摘  要： 首先介紹了CUDA架構特點，在GPU上基于CUDA使用兩種方法實現了矩陣乘法，并根據CUDA特有的軟硬件架構對矩陣乘法進行了優化。然后計算GPU峰值比并進行了分析。實驗結果表明，基于CUDA的矩陣乘法相對于CPU矩陣乘法獲得了很高的加速比，最高加速比達到1 079.64。GPU浮點運算能力得到有效利用，峰值比最高達到30.85%。
關鍵詞： CUDA；矩陣乘法；加速比；峰值比

    隨著多核CPU和眾核GPU的快速發展，計算行業正在從只使用CPU的“中央處理”向CPU與GPU并用的“協同處理”發展，并行系統已成為主流處理器芯片。傳統的GPU架構受其硬件架構的影響不能有效利用其資源進行通用計算，NVIDIA(英偉達)公司推出的統一計算設備架構CUDA(Compute Unified Device Architecturem)，使得GPU具備更強的可編程性，更精確和更高的性能，應用領域也更加廣泛。
    矩陣乘法是一種大計算量的算法，也是很耗時的運算。CPU提高單個核心性能的主要手段比如提高處理器工作頻率及增加指令級并行都遇到了瓶頸，當遇到運算量大的計算，CPU進行大矩陣的乘法就變得相當耗時,運算效率很低下。因此，GPU憑借其超強計算能力應運而生，讓個人PC擁有了大型計算機才具備的運算能力。本文運用GPU的超強計算能力在CUDA架構上實現了大矩陣乘法。
1 CUDA架構
    NVIDIA及時推出CUDA這一編程模型，在應用程序中充分結合利用CPU和GPU各自的優點，特別是GPU強大的浮點計算能力。CPU主要專注于數據高速緩存(cache)和流處理(flow control)，而GPU更多地專注于計算密集型和高度并行的計算。盡管GPU的運行頻率低于CPU，但GPU憑著更多的執行單元數量使其在浮點計算能力上獲得較大優勢[1]。當前的NVIDIA GPU中包含完整前端的流多處理器(SM)，每個SM可以看成一個包含8個1D流處理器(SP)的SIMD處理器。主流GPU的性能可以達到同期主流CPU性能的10倍左右。圖1所示為GPU與CPU峰值浮點計算能力的比較。

    CUDA的編程模型是CPU與GPU協同工作，CPU作為主機(Host)主要負責邏輯性強的事務處理及串行計算，GPU作為協處理器或者設備(Device)負責密集型的大規模數據并行計算。一個完整的CUDA程序=CPU串行處理+GPU Kernel函數并行處理。
    一個CUDA架構下的程序分為兩個部分，即上述的Host端和Device端。通常情況下程序的執行順序如下：Host端程序先在CPU上準備數據，然后把數據復制到顯存中，再由GPU執行Device端程序來處理這些數據，最后Host端程序再把結束運算后的數據從顯存中取回。
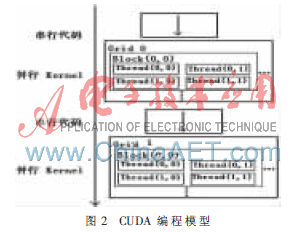
    圖2為CUDA編程模型，從中可以看出，Thread是GPU執行運算時的最小單位。也就是說，一個Kernel以線程網格Grid的形式組織，每個Grid由若干個線程塊Block組成，而每個線程塊又由若干個線程Thread組成。一個Kernel函數中會存在兩個層次的并行，Grid中Block之間的并行和Block中Thread之間的并行，這樣的設計克服了傳統GPGPU不能實現線程間通信的缺點[2]。

    同一個Block下的Thread共用相同的共享存儲器，通過共享存儲器交換數據，并通過柵欄同步保證線程間能夠正確地共享數據。因此，一個Block下的Thread雖然是并行的，但在同一時刻執行的指令并不一定都相同，實現了不同Thread間的協同合作。這一特性可以顯著提高程序的執行效率，并大大拓展GPU的適用范圍。
2 基于CUDA架構矩陣乘法的實現
2.1 一維帶狀劃分
    給定一個M×K的矩陣A和一個K×N的矩陣B，將矩陣B乘以矩陣A的結果存儲在一個M×N的矩陣C中。此種矩陣乘法使用了一維帶狀劃分，每個線程將負責讀取矩陣A中的一行和B中的一列，矩陣進行乘法運算并將計算結果存儲在全局存儲器。
    全局存儲器會對矩陣A進行N次讀取，對矩陣B進行M次讀取。假設數組在每個維度上的尺寸都是BLOCK_SIZE的整數倍。若矩陣大小為32×32，則可表示為(2×16)×(2×16)。下面的內核定義中，結果矩陣C中的每個元素由一個線程負責，for()循環完成A中第X行與B中第X列對應元素的乘加運算，并將結果累加到Cvalue。
      For( int e=0;e < A.width;++e)
      Cvalue+=A.elements[row*A.width+e] *
B.elements[e*B.width+col];
      C.elements[row*width+col]=Cvalue;
      在矩陣相乘實現中，這個內核運算的速度不盡人意，主要瓶頸在于對內存的重復讀取，計算量是2×M×N×K flop，而全局內存的訪問量為2×M×N×K B[3]。若矩陣維數為1 024×1 024，則此次矩陣相乘的計算量就有2 G flop，當矩陣維數更大時，這個運算量就相當大，在內存的讀取上會浪費大量的時間。
2.2 二維棋盤劃分
    因為矩陣A的行和矩陣B的列多次被讀取，為了避免重復加載，選擇把矩陣進行分塊運算，使用shared memory來實現矩陣乘法。運用shared memory的好處在于其延遲小于global memory，并且還能使線程間進行通信。矩陣A只被讀了N/BLOCK_SIZE次，矩陣B僅被讀了M/BLOCK_SIZE次，節省了大量的global memory帶寬。
    首先把劃分的小矩陣塊加載到share memory，則小矩陣本身的乘法就不用去存取外部的任何內存了，因此在二維棋盤劃分中，矩陣乘法的計算量仍然是2×M×N×K flop，b是矩陣B劃分的小矩陣塊的大小，則全局內存訪問量是2×M×N×K/b B。
    棋盤劃分運算可以表示為：C矩陣的(0,0)～(15,15)=A(0～15,0～15)×B(0～15,0～15)+A(0～15,16～31)×B(16～31,0～15)+A(0～15,32～47)×B(32～47,0～15)+…+A(0～15,(16×(n-1)-1)～(16×(n-1))×B((16×(n-1)-1)～(16×(n-1)),0～15)。
        for (int j=0;j<wA;j+=BLOCK_SIZE)
    {    //聲明用于存儲A，B子塊的share memory數組
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];
        }...
        //兩個子塊的乘加，每個線程負責C中一個元素
值的計算
        for (int k = 0; k < BLOCK_SIZE; ++k)
        {
           float t;
           C sub + = As [ ty ] [ k ] * Bs [ k ] [ tx ];
           Cs [ ty ] [ tx ] = C sub;
        }
    __syncthreads();
    ....
    C[(by*BLOCK_SIZE+ty)*wA+bx*BLOCK_SIZE+tx] = Csub;
    dim3 myblock(BLOCK_SIZE,BLOCK_SIZE,1);
    dim3mygrid(((wB+BLOCK_SIZE-1)/BLOCK_SIZE),
(wB+BLOCK_SIZE-1)/BLOCK_SIZE,1);
    根據NVIDIA CUDA Programming Guide，一個Block 里至少要有64個Thread，最多有512個Thread。官方建議256個Thread是最合適的，因為此時有足夠多的active warp有效地隱藏延遲，使得SM能夠盡量滿負荷工作[4]。為便于理解，假設矩陣為n×n ,此時BLOCK_SIZE設置為16，使用dim3來設計，每個Block包含16×16個Thread，一個Grid共有(n/16)×(n/16)個Block。
    BLOCK_SIZE是不是越大越好呢？這樣一個SM里的Thread 就更多，雖然Thread越多越能隱藏 latency，但G80/G92架構每個SM上shared memory僅有16 KB，這會讓每個Thread 能使用的資源更少，效率反而會下降。
2.3 根據CUDA架構對矩陣乘法進行優化

    因為棋盤劃分中涉及到的是二維數組，cudaMalloc2D()能確保分配二維數組并且能分配適當的填充以滿足對齊要求，還能確保在訪問行地址或者二維數組與其他設備內存之間的數據復制能達到最佳性能。
    二維棋盤劃分方法僅限于數組大小必須是BLOCK_SIZE的整數倍，若矩陣維數并不是16的整數倍，則會造成運算效率的下降，此時可以利用CUDA架構特點和CUDA提供的cudaMallocPitch()函數來解決此問題。cudaMallocPitch()可以自動地以最佳倍數來分配內存。
    呼叫Kernel部分需要修改成：
    matrixMul<<<mygrid,myblock>>>(d_A,d_B,d_C,wA,wB,
d_pitchA/sizeof(float),d_pitchB/siz
eof(float),d_pitchC/sizeof(float));
    cudaMalloc部分改成：
      float* d_A;
cutilSafeCall(cudaMallocPitch((void**)&d_A,&d_pitchA,
wA*sizeof(float),wB));
      float* d_B;
cutilSafeCall(cudaMallocPitch((void**)&d_B,&d_pitchB,
wB*sizeof(float),wA));
      float* d_C;
cutilSafeCall(cudaMallocPitch((void**)&d_C,&d_pitchC,
wB*sizeof(float),wB));
    矩陣內存與顯存之間的讀取都需要做相應的修改：    
cutilSafeCall(cudaMemcpy2D(d_A,d_pitchA,A,wA*sizeof(float),
wA*siz
eof(float),wB,cudaMemcpyHostToDevice));    
cutilSafeCall(cudaMemcpy2D(d_B,d_pitchB,B,wB*sizeof(float),
wB*sizeof(float),wA,cudaMemcpyHostToDevice));
cutilSafeCall(cudaMemcpy2D(C,wB*sizeof(float),d_C,d_pitchC,
wB*sizeof(float),wB,cudaMemcpyDeviceToHost));
    在數值分析，Kahan求和算法(也稱作補償總和)能顯著減少浮點數運算的誤差，在CUDA矩陣乘法中可以通過使用Kahan求和算法來提高計算精準度[5]。算法如下：
    for (int k = 0; k < BLOCK_DIM; ++k)
    {
            float t;
        comp -= AS[ty][k] * BS[k][tx];
        t = Csub - comp;
        comp = (t - Csub) + comp;
        Csub = t;
    }
3 測試環境及實驗結果
    測試的硬件環境：CPU使用的是AMD Athlon II X2 245處理器,核心數為2，該處理器主頻為2.9 GHz，峰值運算能力約為17.4 GFLOPS；GPU使用的是NVIDIA GeForce 9800M GTS，有8個SM即有64個SP單元，顯存帶寬為51.2 GB/s，GPU核心頻率為0.625 GHz，單精度浮點計算能力為240 GFLOPS，屬于NVIDIA中端顯卡。測試的軟件環境：Windows XP系統，CUDA toolkit 3.0,Visual Studio 2008，CUDA計算能力為1.1。
    在程序運行的測試中，對矩陣規模由256×256～2 048×2 048逐漸增大，實驗數據均是三次測試取得的平均值，這樣實驗的結果更準確。加速比是指程序在CPU上運行的時間與程序在GPU上運行所需的時間之比。峰值比是指運算速度與GPU單精度浮點運算能力之比。最后求得在各種矩陣規模運行下的加速比及峰值比。實驗結果如表1所示。

    實驗結果表明：當矩陣維數小于320×320時，帶狀劃分加速比小于1，說明CPU運算時間要小于一維帶狀劃分時GPU的運算時間，這說明GPU計算時，從內存復制矩陣到顯存和把結果矩陣從顯存拷貝回內存過程中消耗了一些時間[6]。隨著矩陣維數的增大，CPU的運算時間呈現級數增長，而GPU運算時間只是小幅度增長。此時GPU強大的浮點運算能力凸顯出來，加速比在矩陣維數為2 048時最大為1 079.64，CPU上Intel MKL矩陣乘法比文中所用的CPU矩陣乘法快了200多倍，但是依靠GPU流多處理的并行執行能力，GPU上的實現方法還是比Intel MKL快了5倍左右。運用CUDA的軟硬件架構使得GPU合理組織數據，使得內存的讀取節省了大量時間。峰值比也有很大的提高，峰值比說明了算法對GPU強大浮點運算能力的利用，對GPU相應算法的對比具有很高的參考價值。
    通過矩陣乘法在CPU與GPU上不同的性能表現可以發現，NVIDIA公司推出的CUDA使某些大運算量的計算可以從大型計算機或者超級計算機轉移到個人PC，這一新技術不僅使科研縮減了成本，同時也為科學領域進行大規模運算提供了新方法[7]。對于它的未來值得期待，畢竟CUDA已經在影視制作、計算金融、流體力學、醫學成像、石油天然氣數據收集、地質勘探及超級計算機的建立等領域取得了成功。
參考文獻
[1] NVIDIA Corporation.NVIDIA CUDA Programming Guide  Version3.0[EB/OL].(2010-02-10)[2011-08-20].http://cuda.csdn.net/.
[2] 張舒，褚艷利，趙開勇，等.GPU高性能并行運算之CUDA[M].北京：中國水利水電出版社，2009.
[3] Ye Zhenyu.GPU assignment 5KK70[DB/OL].(2009-11-05)[2011-09-01].http://wenku.baidu.com/view/9cd2e372027-68e9951e738e5.html.
[4] NVIDIA Corporation.NVIDIA CUDA CUBLAS library PG-00000-002_V3.0[EB/OL].(2010-02-10)[2011-09-10].http://cuda.csdn.net/.
[5] Hotball.深入淺出談CUDA技術[DB/OL].(2008-11-21) [2011-09-15].http://www.pcinlife.com/article/graphics/2008-06-04/1212575164d532_3.html.
[6] 劉進鋒，郭雷.CPU與GPU上幾種矩陣乘法的比較與分析[J].計算機工程與應用，2011,47(19)：9-23.
[7] 肖江，胡柯良，鄧元勇.基于CUDA的矩陣乘法和FFT性能測試[J].計算機工程，2009.35（10）：7-10.