文獻標識碼: A
文章編號: 0258-7998(2015)03-0082-04
隨著網絡業務種類的增加,如何提高網絡流量預測精度具有十分重要的意義[1]。網絡流量預測傳統模型主要包括:線性回歸、泊松過程、時間序列等[2-3],它們可以對短期的網絡流量數據進行預測,但現代網絡流量變化規律相當復雜,因此傳統預測模型的精度有待進一步提高。
隨著非線性理論發展,出現了以BP神經網絡(BP neural network,BPNN)為代表的網絡流量非線性預測模型,其具有較好的非線性預測能力,可以對網絡流量變化特點進行準確跟蹤,提高了網絡流量的預測精度[4]。然而,在實際應用過程中,BP神經網絡的預測性能與其參數密切相關[5]。為此,有學者提出采用人工魚群算法、遺傳算法、人工螢火蟲算法、粒子群算法、蟻群算法等對BP神經網絡參數進行優化[6-8],一定程度較好解決BP神經參數優化的難題,但是這些算法均有各自不同程度的不足[9]。布谷鳥搜索(cuckoo search,CS)算法是一種新型群體智能算法,具有簡單、高參數少、易于實現的特點,在模式識別、組合優化等領域得到了廣泛的應用[10]。
為了提高網絡流量預測精度,針對BP神經網絡參數優化的難題,本文提出一種CS-BPNN的網絡流量預測模型。仿真實驗表明,本文模型獲得更加理想的網絡流量預測結果。
1 相空間重構和BP神經網絡
作為CS-BPNN算法的研究基礎,本節主要描述下相空間重構與BP神經網絡的基礎知識,這些知識在相關的文獻都有詳細的介紹[11]。
1.1 相空間重構

式中,子為延遲時間、m為嵌入維數;X(i)表示重構后的相點[12]。
1.2 BP神經網絡算法
設一個網絡流量動力系統的輸入為式(1),則構造輸出函數為y(i)=x(i+1),BP神經網絡的輸入節點數是網絡流量的嵌入維數m、隱層節點數是p、輸出個數是1,通過f:Rn→R構建映射[13]。隱層各節點的輸入是:

式中,vj表示從隱層到輸出層的連接權值;表示輸出層的閾值。
2 CS-BPNN的網絡流量預測模型
2.1 布谷鳥搜索算法
2009年,YANG等模擬布谷鳥尋窩產卵的行為方式,提出布谷鳥搜索(Cuckoo Search,CS)算法[14]。設x為第i個鳥巢在第k代的鳥巢位置,L(λ)為Levy隨機搜尋路徑,則布谷鳥尋巢的路徑和位置更新方式為:

采用3個準測試函數對布谷鳥CS算法和粒子群算法PSO(Particle Swarm Optimization)的性能進行對比測試,各測試函數的數學表達式如表1所示。兩種算法的運行結果如圖1所示。對圖1進行分析可以看出,CS算法的性能均優于粒子群算法(PSO)算法,對比結果表明,CS算法加快算法收斂速度,在一定程度上防止多峰問題易陷入局部最優的不足,提高了算法的搜索能力,獲得了更優的結果。


2.2 布谷鳥算法優化BP神經網絡參數步驟
(1)初始化鳥巢數n、Pa及最大迭代次數Nmax等參數。
(2)隨機產生n個鳥巢的初始位置,它們與BP神經網絡初始閾值和連接權值相對應,BP神經網絡根據參數值對訓練集進行訓練,并計算預測結果。

3 CS-BPNN在網絡流量預測中的應用
3.1 數據來源
為了測試CS-BPNN的有效性,選擇行內的標準數據:http://newsfeed.ntcu.net/~news/2013的8月1日到8月30日的每小時流量作為仿真對象,具體如圖2所示。選擇620個數據進作為訓練集,用CS-BPNN進行訓練,建立網絡流量預測模型;其余100個數據作為測試集,測試模型性能。

3.2 對比模型及評價標準
由于粒子群算法(PSO)在BPNN參數應用比較廣泛,為了使CS-BPNN預測結果具有可比性,選擇粒子群算法優化(PSO-BPNN)進行對比實驗,模型性能優劣采用均方根誤差(RMSE)和平均絕對百分誤差(MAPE)進行評價。
3.3 學習樣本構建
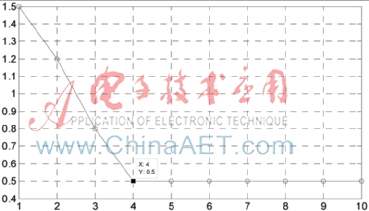
首先采用耦合簇方法C-C(Coupled Cluster method)計算網絡流量最優的延遲時間τ,具體如圖3所示,其中橫坐標表示延遲時間,縱坐標表示關聯積分。從圖3可知,最優延遲時間τ=4,然后利用Cao方法[15]求嵌入維數,結果如圖4所示,其中橫坐標表示延遲時間,縱坐標表示最大熵值。從圖4可知,網絡流量時間序列相空間重構的最小嵌入維數m=5,采用τ=4和m=5重構網絡流量,得到CS-BPNN的學習樣本。

3.4 結果與分析
采用PSO、CS找到的BPNN最優參數,建立基于PSO-BPNN、CS-BPNN的網絡流量預測模型,然后用測試集進行預測,各模型的預測結果如圖5所示。從圖5可知,相對于PSO-BPNN,CS-BPNN提高了網絡流量的預測精度,預測偏差更小,對比結果,CS-BPNN融合CS算法的全局搜索能力和BPNN的非線性預測,可以對網絡流量變化趨勢準確跟蹤,預測結果更加穩定、可靠。
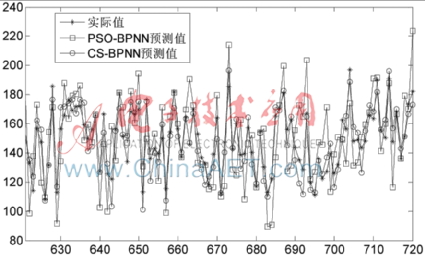

PSO-BPNN、CS-BPNN的網絡流量預測結果的MAPE和RMSE見表2。從表2可知,相對于PSO-BPNN,CS-BPNN預測誤差更小,預測精度更高,對比結果表明,CS-BPNN建立了預測精度更高的網絡流量預測模型。
4 含噪網絡流量的測試
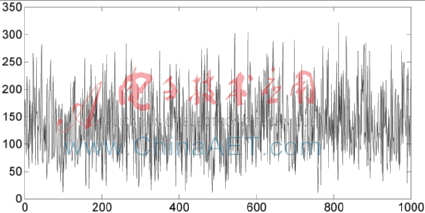
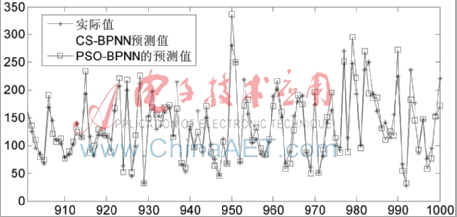
為了測試CS-BPNN模型的魯棒性,采用一個含有噪聲網絡流量進行仿真實驗,以測試模型的魯棒性,含噪的網絡流量數據如圖6所示。對含噪的網絡流量數據進行建模與預測,不同模型的網絡流量預測結果如圖7和表3所示。從圖7和表3可知,相對于比模型,CS-BPNN獲得了更加理想的預測結果,這表明CS-BPNN具有較強魯棒性,具有一定的抗噪能力。

5 結束語
由于影響因素復雜、多變,導致網絡流量具有非線性、混沌性,傳統方法難建立準確的預測模型,而BP神經網絡也受到參數的不利影響。為了獲得理想的預測結果,本文提出了一種網絡流量預測模型CS-BPNN,并通過具體仿真實驗測試模型性能。結果表明,CS-BPNN解決了BP神經網絡參數優化問題,建立了預測精度高、效果好的網絡流量預測模型,同時為其他非線性時間序列提供了一種預測建模新思路。
參考文獻
[1] SILVA C G.Time series forecasting with a nonlinear model and the scatter search meta-heuristic[J].Information Sciences,2008,178(16):3288-3299.
[2] 姜明,吳春明,胡大民,等.網絡流量預測中的時間序列模型比較研究[J].電子學報,2009,37(11):2353-2358.
[3] 高波,張欽宇,梁永生,等.基于EMD及ARMA的自相似網絡流量預測[J].通信學報,2011,32(4):47-56.
[4] 劉百芬,熊南.基于動態加權LS-SVM的網絡流量混沌預測[J].電視技術,2013,37(7):87-90.
[5] ESTE A,GRINGOLI F,SALGARELLI L.Support vector machines for TCP traffic classification[J].Computer Networks,2009,53(14):2476-2490.
[6] QI H L,ZHAO H,LIU W W,ZHANG H B.Parameters optimization and nonlinearity analysis of grating eddy currentdisplacement sensor using neural network and genetic algo-rithm[J].Journal of Zhejiang University Science A,2009,10(8):1205-1212.
[7] CALLADO A,KEU R J,SADOK D,et a1.Better network traffic identification through the independent combination of techniques[J].Journal of Network and Computer Applica-tions,2010,33(4):433-446.
[8] 劉淵,戴悅,曹建華.基于小波神經網絡的流量混沌時間
序列預測[J].計算機工程,2008,34(16):105-106.
[9] 趙振江.基于PSO-BP神經網絡的網絡流量預測與研究[J].計算機應用與軟件,2009,26(1):218-211.
[10] YANG X S,DEB S.Engineering optimization by cuckoo search[J].International Journal of Mathematical Modeling and Numerical Optimization,2010,1(4):330-343.
[11] 高述濤.CS算法優化BP神經網絡的短時交通流量預測,計算機工程與應用,2013,49(9):106-109.
[12] 王升輝,裘正定.結合多重分形的網絡流量非線性預測[J].通信學報,2007,28(2):45-50.
[13] 李松,羅勇,張銘銳.遺傳算法優化BP神經網絡的混沌時間序列預測[J].計算機工程與應用,2011,47(29):52-55.
[14] 王凡,賀興時,王燕,等.基于CS算法的Markov模型及收斂性分析[J].計算機工程,2012,38(11):180-182,185.
[15] CAO L J.Support vector machines experts for time series forecasting[J].Neurocomputing,2003,51:321-339.

