文獻標識碼: A
文章編號: 0258-7998(2015)02-0156-04
0 引言
應用功率因數校正(PFC)技術時,工作在電流連續模式(CCM)的變換器多應用于大功率的應用場合。這些變換器有很高的功率因數和很快的瞬態響應[1],但在高電壓輸入輕載輸出時,輸出電容需要承受很高的電壓應力[2]。對于小功率應用,工作在斷續模式(DCM)的變換器更為合適,該變換器的電流諧波小,控制環路設計簡單,但其峰值電流偏大,開關管與電感都需要承受很大的電流應力和導通損耗。使用峰值電流控制的臨界模式(BCM)變換器開關管在電感電流為零時開啟,開關管損耗和電磁干擾較小,并且輸出二極管不會有反向恢復問題[3-4],相當于DCM模式,工作在BCM模式下的變換器的開關管、電感電流應力和損耗較小。
臨界模式PFC建模的難點在于,穩態時開關頻率和占空比并不固定,確定電路靜態工作比較困難[5],通常采用準穩態近似分析[6]。已有的建模方法中[7-8]分別利用平均開關模型法和對線電壓半周期輸出功率求平均的方法建立了臨界模式模型,但得出的傳遞函數包含有電壓轉換比或正弦變化的輸入電壓這些時變量,這給電壓環路設計造成了困難。
本文針對反激PFC變換器,分析它在臨界模式下的工作過程,推導出輸入電流畸變與電壓轉換比、輸出功率的變化關系式,并且建立了控制量與輸出二極管的輸出電流iD的約束關系,通過先后對iD在開關周期和線電壓半周期平均的方法,分別消去占空比D與正弦輸入電壓兩個時變量,經過線性化后,得到小信號模型。同時,基于建立的模型,設計了控制環路并制作一臺30 W反激PFC樣機進行驗證。
1 臨界模式電路的工作原理

圖1是反激PFC變換器簡化電路。控制電路由乘法器、零電流檢測電路和PI調節器等構成。
為了方便分析,對電路進行以下的假設:輸入電壓為理想的正弦波,經過整流橋后,不會產生損耗和交越失真,輸入電壓的瞬時值可以表示成vg(t)=Vm|sin(wt)|,Vm為輸入正弦波的幅值;變換器的開關頻率fs遠遠大于線電壓的頻率f2L,在一個開關周期中線電壓vg和輸出電壓v近似恒定,可以認為電路工作在準穩態;變換器電壓環帶寬選擇足夠小(fband>>f2L),補償器的輸出在1/2線電壓周期內基本不變。
因此變換器的開關周期Ts表達式為:

2 輸入電流畸變分析
在穩態時,電感平均電流跟隨輸入電壓變化,則開關周期內電感電流峰值的表達式為:ipk(t)=Ipk|sin(wt)|,其中Ipk是線電壓周期內電感電流峰值。輸入電流在一個開關周期里的平均值iin與電感電流峰值ipk的關系為:
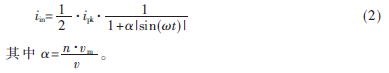
從圖1可以得到電感電流控制函數:
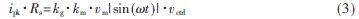
其中,kg為電阻分壓器的分壓系數,km是乘法器的增益,vctrl是補償電路的輸出。
通常情況下,PFC補償器帶寬較窄,可以認為在一個線電壓周期內vctrl近似恒定,等于Vctrl。考慮線電壓半周期,輸入平均電流的表達式可改寫為:

其中,![0YZ}X%DS6HRY8AJN{]NT)TD.jpg 0YZ}X%DS6HRY8AJN{]NT)TD.jpg](http://files.chinaaet.com/images/2015/08/06/6357449377443100009541996.jpg) 。顯然,變換器的輸入電流波形的畸變程度受到大小的影響。
。顯然,變換器的輸入電流波形的畸變程度受到大小的影響。
3 小信號模型的建立
為了消除輸入電壓與二極管電流兩個時變量影響,需要建立輸入/輸出電壓、電壓環路輸出及輸出二極管電流約束關系。
在一個開關周期內,輸出二極管上的平均電流的表達式為:

假設vm變化的速度遠遠低于線電壓周期,將式(3)代入式(5)中可以得到控制電壓Vctrl、輸入峰值電壓Vm、輸出電壓v與二極管平均輸出電流iD的關系表達式,并對各變量在線電壓半周期內進行平均,可以得到:
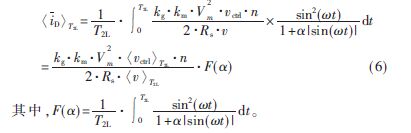
計算![VC[[Z_)NKKGWI6]}JXX}MTJ.jpg VC[[Z_)NKKGWI6]}JXX}MTJ.jpg](http://files.chinaaet.com/images/2015/08/06/6357449389955700005556248.jpg) 解析表達式比較復雜,利用計算機進行計算可以很容易得到滿足精度要求的數值解。
解析表達式比較復雜,利用計算機進行計算可以很容易得到滿足精度要求的數值解。
為了建立小信號模型,假設輸入線電壓的峰值、輸出電壓和控制電壓的直流分量遠遠大于交流分量,即:
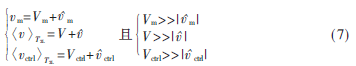
將式(7)帶入式(6)中,忽略高次項,就可以得到線性小信號表達式:

其中:
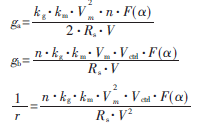
利用相同的方法可以得到臨界模型Boost拓撲PFC電路的小信號表達式:

其中:

根據式(9)并考慮輸出電容串聯等效電阻,可以得到的小信號輸出電路,如圖2所示。
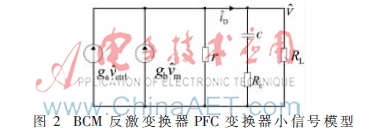
由圖2可以得到新功率級和泛音衰減函數:
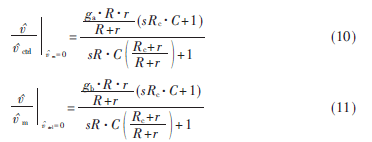
為了進一步確定小信號模型的參數,需要求出穩態Vctrl和km的值。km值是模擬乘法器增益系數,可以從控制芯片的數據手冊中得到相關的參數,例如UCC28810中km的大小為0.69。而Vctrl要根據相應的拓撲結構來求解,如反激變換器可以做以下的推導。
假設電路處于穩態:(1)負載固定,輸出功率恒定,在線電壓半周期內輸入的能量等于輸出的能量;(2)開關頻率fS遠大于線電壓頻率f2L,所以輸入電流的瞬時值近似等于一個開關周期內線電流平均值。
由此可得到:

將式(4)代入式(12)得到:
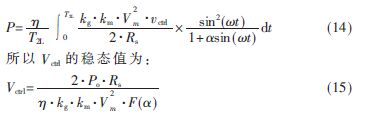
4 電壓環路設計與驗證
本文設計了一款30 W的反激PFC來研究驗證建立的模型,樣機使用的電路參數如表1所示。

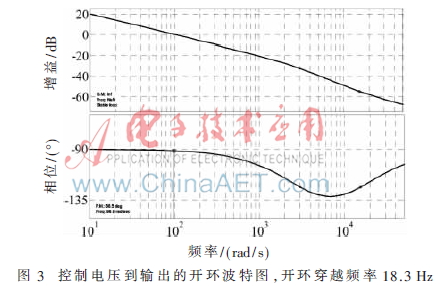
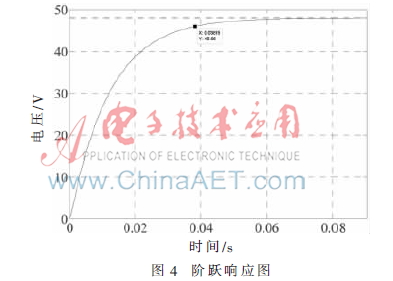
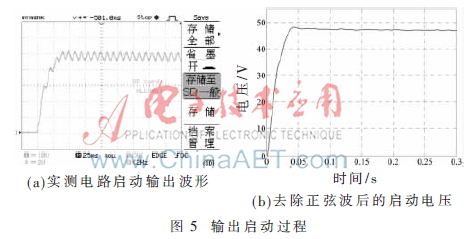
根據表1參數建立的模型,經過補償后的波特圖如圖3所示。其穿越頻率為18.3 Hz,相位裕度為88.5°。圖4為建立模型的階躍響應圖,響應時間為31 ms。圖5(a)為實測電路啟動輸出波形,圖5(b)為去除正弦紋波后啟動電壓曲線,實測啟動時間為30 ms。負載電阻從500 Ω切換為80 Ω時輸出電壓波形如圖6所示,由圖中可知輸出的響應時間為33 ms。

5 結論
本文針對臨界模式PFC電路進行分析建模,通過建立輸入/輸出電壓、電壓環路輸出以及輸出二極管電流等變量約束關系,在半線電壓周期內對這些變量作平均化處理,消除輸入電壓與二極管電流兩個時變量影響,進而得到電路的傳遞函數和小信號等效電路。得到的傳遞函數和小信號模型表明:由于存在電流內環,電感電流平均值完全受到Ic的控制,故電感電流為非獨立變量,而只作為等效受控源存在。所以工作在臨界模式下的PFC變換器的小信號模型是一階電路,且小信號等效電路中不會出現電感。
根據建立的小信號模型設計了補償電路,并制作了實驗樣機。從理論仿真與實際電路性能數據對比可知,瞬態響應時間的理論值與實測值比較接近;理論計算中輸出電壓不會出現紋波,而實際輸出中存在100 Hz電壓紋波。這是由于建模過程對輸出二極管的電路進行了積分,消除了紋波干擾。利用該方法建立的模型為低頻模型,但對于環路帶寬較窄的PFC電路,該模型可以比較準確地描述電路傳遞函數的特性,借助該模型可以很好地完成對臨界模式下PFC變換器的環路設計。
參考文獻
[1] LAI Z,SMEDLEY K M.A family of continuous-conduction-mode power-factor-correction controllers based on the general pulse-width modulator[J].Power Electronics,IEEE Transactions on,1998,13(3):501-510.
[2] DENG W,ZHANG B,HU Z.Analysis of a novel boundary conduction mode(BCM) and voltage control of buck capacitorin single-stage PFC circuit[C].Power Electronics and MotionControl Conference,2004.IPEMC 2004.The 4th International.IEEE,2004,1:126-131.
[3] 楊飛,阮新波,楊洋,等.采用耦合電感的交錯并聯電流臨界連續Boost PFC變換器[J].電工技術學報,2013,28(1):215-224.
[4] 楊飛,阮新波,季清,等.采用耦合電感的交錯并聯電流臨界連續Boost PFC變換器輸入差模EMI分析[J].電工技術學報,2013,28(3):202-214.
[5] SUNTIO T.Unified average and small-signal modeling of direct-on-time control[J].Industrial Electronics,IEEE Trans-actions on,2006,53(1):287-295.
[6] CHEN J,ERICKSON R,MAKSIMOVIC D.Averaged switch modeling of boundary conduction mode dc-to-dc converters[C].Industrial Electronics Society,2001.IECON′01.The 27th Annual Conference of the IEEE.IEEE,2001,2:844-849.
[7] KI S K,LU D D C.Implementation of an efficient trans-formerless single-stage single-switch AC/DC converter[J].Industrial Electronics,IEEE Transactions on,2010,57(12):4095-4105.
[8] CHEN J,CHANG J.Analysis and design of SEPIC con-verter in boundary conduction mode for universal-line power factor correction applications[C].Power Electronics Specialists Conference,2001.PESC.2001 IEEE 32nd Annual.IEEE,2001,2:742-747.

