摘  要： 在總結維基百科特點的基礎上，調研了國內外使用維基百科計算語義相關度的算法。根據這些算法的特點，對其進行了系統的分類，并列舉了每個分類下的經典算法。

　　關鍵詞： 維基百科；相關度；算法

0 引言

　　相關度是指事物之間相關聯的程度，而語義相關度是指概念之間相關聯的程度。計算語義相關度是非常復雜的，因為它需要用到豐富的語義知識，也要對不同的關系給出不同的權重值。在語義信息處理的相關研究中，很多研究者利用語料庫的相關統計信息獲取語義相關度信息，也有研究者利用WordNet等語義網絡來衡量詞或者概念之間的語義相關度。近年來，很多研究都證明維基百科是計算語義相關度的一個好資源。

　　最先利用維基百科進行語義相關度研究的是STRUBLE M和PONZETTO S P[1]，他們把應用在WordNet上效果比較好的一些經典算法應用到維基百科中，實驗結果表明，在大數據集上，在維基百科的效果要好于在WordNet的效果。隨后，ZESCH J和GUREVYC I[2]對維基百科的分類圖和文檔圖進行了圖論分析并與GermaNet進行了比較，同樣證明了維基百科可以作為一種語義知識資源代替一些傳統的語義網絡，將自然語言處理的一些經典算法應用到維基百科中是可行的。

　　本文對維基百科進行了研究，對利用維基百科計算語義相關度的算法進行了調研，最后總結了幾種典型算法的特點并進行了分類。

1 維基百科

　　維基百科于2001年被發起，現在，它涵蓋了藝術、地理、歷史、自然科學等領域，包括了200多種語言的版本，注冊用戶達5000多萬。它作為互聯網上最大的最廣泛使用的免費的百科全書，擁有超過百萬的解釋頁面，更新速度快。本文從以下兩方面對維基百科進行系統的介紹。

　　1.1 維基百科中的條目

　　條目，即頁面，是維基百科基本的組成單位。為了提高一致性，條目的編輯需遵循一系列的編輯規則，其主要的規則有以下6條[3]：

　　（1）一個條目只描述一個概念，一個概念只有一個條目與之對應；

　　（2）條目的標題是簡潔的短語，類似于傳統敘詞表中敘詞；

　　（3）同義詞通過重定向鏈接連接；

　　（4）消歧義條目為用戶提供可選擇的多種語義；

　　（5）條目的開始是對主題的簡單介紹，第一句定義了概念及其類型；

　　（6）條目中有超鏈接，這些超鏈接表示了該條目與其他條目之間的關系。

　　根據這些編輯規則，將維基百科中的條目分為：分類條目、重定向條目、消歧義條目以及解釋條目。其中分類條目是維基百科中的分類索引，重定向條目和消歧義條目對應規則（3）和（4），解釋條目對應編輯規則（1）。

　　1.2 維基百科中的超鏈接

　　普通的語料庫和網絡語料最大的不同點就是網絡語料庫具有超鏈接，而超鏈接提供了一個頁面跳轉到另一個頁面的功能。維基百科就是典型的網絡語料庫。維基百科鏈接結構密集，平均每個條目擁有20個超鏈接，而且超鏈接還蘊含了豐富的語義信息。一般按照超鏈接的方向把超鏈接分為兩大類：一類是前向鏈接，另一類是后向鏈接。如圖1所示，前向鏈接是指源頁面連接另外一個頁面的鏈接，后向鏈接是指一個頁面連接源頁面的鏈接。

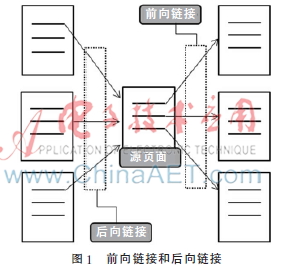
　　除此之外，也可以根據超鏈接所連接的頁面類型進行分類，分別為語言間的鏈接（Interlanguage Links）、分類與子類之間的鏈接（Category to Subcategory）、分類與解釋頁面之間的鏈接（Category to Article）、重定向頁面（Redirect to Article）與解釋頁面之間的鏈接（Article to Article）。根據這種分類可以初步判斷錨文本之間的關系（錨文本是超鏈接的文本部分，用戶通過點擊這個文本就可到達目標頁面）。

　　2 基于維基百科的語義相關度算法

　　2.1 基于統計學的語義相關度算法

　　2.1.1 詞匯共現法

　　詞匯共現法是基于統計學的方法來計算語義相關度的經典方法。由于詞匯共現在敘詞表構建的研究中已經被廣泛地證明是有效的，因此把它應用到維基百科中可能也是可行的。兩個詞匯的詞匯同現率可以用下面的公式進行粗略的定義：

　　其中，D是包含t1的文檔的集合。為了度量兩個詞的相關度，該方法使用了包含這兩個詞的文檔數。具體的比較經典的方法有共現文檔數方法（SD）[4]、文字覆蓋法（TO）。

　　共現文檔數就是在一個較大的語料庫中利用詞出現的文檔數，如Jaccard公式：

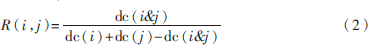
　　其中，dc（i）、dc（j）分別表示包含鏈接i、j的文檔數，dc（i&j）表示既包含i也包含j的文檔數。

　　文字覆蓋法就是通過在2個詞各自的定義文本中共同出現的文本來計算相關度。比較經典的算法有Lesk算法[5]。在維基百科中，可以尋找在解釋文檔中的共現詞并利用式（3）來計算：

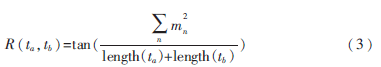
　　其中，n表示文檔ta和tb中都出現的文本片段（可能是一個詞或連續的多個詞），mn表示每個片段的詞數，length（ta）和length（tb）表示兩個文檔的總詞數。

　　2.1.2 鏈接共現法

　　盡管上文中的詞匯共現法已被證明是有效的，但是由于語義分析的復雜性，自然語言處理仍然存在很多準確性的問題。所以有人提出了鏈接共現的方法，這種方法只使用語義網絡中的鏈接來避免自然語言處理中的準確率的問題。因為語義網絡是一個概念與鏈接的集合，所以使用鏈接同現法是有意義的。具體的公式和詞匯共現的公式的道理是一樣的，不同點只是使用文檔的鏈接代替詞匯。

　　比較經典的鏈接共現的方法是GABRILOVICH E[6]提出的TF-IDF的方法。TF-IDF使用了兩個度量值：TF（Term Frequency）詞匯頻率和IDF（Inverse Document Frequency）后向文檔頻率。這種方法是通過計算維基百科頁面中鏈接的權值得到相應概念的向量，然后通過比較概念向量來計算兩個概念的相關度。一個文檔中鏈接的權值的計算公式如下：

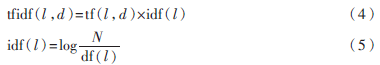
　　其中，tf（l，d）表示在文檔d中鏈接l出現的次數，N表示維基百科中文檔的數量，df（l）是包含鏈接l的文檔的數量。簡單來說，權值隨著文檔d中鏈接出現的頻率遞增。但是總的來說，因為每個維基百科的頁面都有自己的URL而且都對應了一個概念，所以計算兩個鏈接的相關度等同于計算兩個概念的相關度。

　　2.2 基于維基百科路徑的語義相關度算法

　　維基百科網絡詞匯集，是一個由條目和超鏈接組成的集合，它的結構是一個有循環的圖，概念就是圖的節點，超鏈接就是圖的邊，所以它就可以用一個圖的形式來表示：G={V，E}（V：維基百科中的條目/概念集合，E：維基百科中超鏈接的集合）。在考慮如何計算任意一個條目對vi和vj之間的相關度時，NAKAYAMA K等人[7]假設影響它們之間相關度主要有以下兩個因素：

　　（1）從條目vi到條目vj的路徑的數量；

　　（2）每一條從條目vi到條目vj的路徑長度。

　　如果有很多路徑可以從條目vi到達條目vj，那么它們之間的相關度相對較強。另外，兩個條目之間的相關度還受路徑長短的影響。換句話說，如果在圖G中從條目vi到達條目vj的路徑相對較短，那么它們之間的相關度要高于相對較長的。因此，如果從條目vi到達條目vj的所有路徑為P={p1，p2，...，pn}，NAKAYAMA K將它們之間的PF（Path Frequency）定義為：

　　其中，d（lenpk）是一個以路徑pk的長度為變量的單調遞增函數，例如對數函數的單調遞增函數都可用作函數  d（lenpk）。

　　而且根據統計發現，在計算相關度時必須考慮維基百科的鏈接結構的分布特征，例如這樣一種條目，有很多條目都擁有到達該條目的超鏈接。如果只是用PF的方法，那么這類條目會與很多條目具有較強的相關度。然而通常情況下該類條目對應的概念是普通的比較綜合的大眾的概念。因此，必須考慮這類條目的后向鏈接，NAKAYAMA K定義了IBF（Inversed Backward Frequency），IBF與PF組合形成了PF-IBF方法：

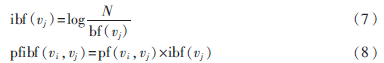
　　其中，N表示所有的條目數，bf（vj）表示條目vj的后向鏈接數。從上文的PF-IBF公式可以看出，如果條目vi和vj條目通過前向或后向鏈接相連并且vj沒有后向鏈接，則相應的pfibf值就會很高，概念之間的相關度相對較大。

3 結論

　　維基百科作為世界上最大的在線百科全書，蘊含了豐富的語義知識。本文總結了利用維基百科完成復雜的語義相關度計算的方法，使用這些算法可以更容易地完成對維基百科的知識挖掘和完成文本分類等工作。但目前，無論是對維基百科使用的研究，還是維基百科相關算法研究，我國都遠遠少于國外。今后，隨著維基百科的優勢顯現，相信會有更多的國內專家關注維基百科，維基百科的相關技術也會更加成熟。

參考文獻

　　[1] STRUBE M， PONZETTO S P. WikiRelate! Computing semantic relatedness using Wikipedia[C]. AAAI， 2006，6： 1419-1424.

　　[2] ZESCH T， GUREVYCH I. Analysis of the Wikipedia category graph for NLP applications[C]. Proceedings of the TextGraphs-2 Workshop （NAACL-HLT 2007）， 2007：1-8.

　　[3] MEDELYAN O， MILNE D， LEGG C， et al. Mining meaning from Wikipedia[J]. International Journal of Human-Computer Studies， 2009，67（9）：716-754.

　　[4] BANERJEE S， PEDERSEN T. Extended gloss overlaps as a measure of semantic relatedness[C]. IJCAI， 2003，3：805-810.

　　[5] LESK M. Automatic sense disambiguation using machine readable dictionaries： how to tell a pine cone from an ice cream cone[C]. Proceedings of the 5th Annual International Conference on Systems Documentation， ACM， 1986：24-26.

　　[6] GABRILOVICH E， MARKOVITCH S. Computing semantic relatedness using Wikipedia-based explicit semantic analysis[C]. JCAI， 2007，7：1606-1611．

　　[7] NAKAYAMA K， HARA T， NISHIO S. Wikipedia mining for an association Web thesaurus construction[M]. Web Information Systems Engineering-WISE 2007， Springer Berlin Heidelberg， 2007： 322-334.