文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2016.04.006
中文引用格式: 李安壽,陳琦,王子才,等. 分布式電源系統中的非線性因素分析[J].電子技術應用,2016,42(4):22-24.
英文引用格式: Li Anshou,Chen Qi,Wang Zicai,et al. Nonlinear factors analysis of distributed power system[J].Application of Electronic Technique,2016,42(4):22-24.
0 引言
與集中式電源系統相比,分布式電源系統具有可靠性高、便于模塊化、標準化、集成化、易擴展、易維護等許多優點[1]。因此,分布式電源系統在航天器電源、航空電源、電力系統、船舶、新能源汽車、計算機電源等領域得到了長足發展和廣泛應用。然而,分布式電源系統結構多樣,是非常復雜的非線性系統,尚未形成完善的設計和分析方法。本文介紹了分布式電源系統建模方法,對分布式電源系統中可能存在的非線性影響因素進行了歸納總結,為下一步研究奠定了基礎。
1 分布式電源系統中的幾種連接方式
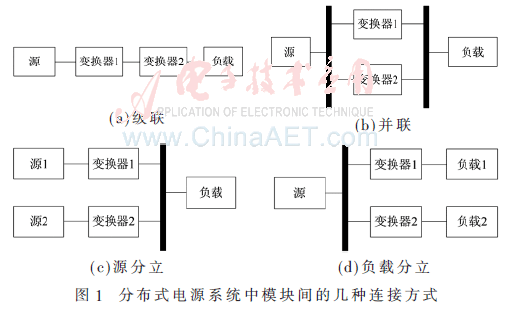
分布式電源系統的拓撲結構可以看成“源+變換器+負載”。各模塊間可以有以下幾種連接方式[2]:(1)級聯;(2)并聯;(3)源分立;(4)負載分立(如圖1所示)。另外,分布式電源系統各模塊間還有串聯連接方式,由于這種連接方式并不常見,本文未予列出。由圖1所示的連接方式可以組成更為復雜的分布式電源系統。這些不同的連接方式,使得分布式電源系統的設計和分析都比較復雜,同時也容易引起系統不穩定的問題[3]。
2 分布式電源系統的建模方法
對一個開關變換器而言,可以采用器件級模型盡可能準確地分析開關變換器的詳細特性。但對于整個分布式電源系統而言,使用器件級模型來分析整個系統的特性是十分困難的。根據不同的需求,人們經常會從平均、功率守恒等觀點出發采用簡化模型來對分布式電源系統進行研究。在分布式電源系統的仿真分析中,大信號平均模型是一種相對合適的模型,它保留了系統的非線性特性,仿真時間較短。為了進一步降低分布式電源系統分析的難度,人們也提出了更為簡化的模型:在分析兩個級聯的開關變換器時,后級變換器經常等效為一個簡單的恒功率負載[4]或恒阻負載和恒功率負載的組合[5]。在靜態模型的基礎上,文獻[6]則進一步建立了恒功率負載的高階動態模型。
在分布式電源系統中,經常把負載和變換器等效成為一個新的“負載”,負載是有源和無源功率器件的組合,這使得分布式電源系統的負載多種多樣。概括起來,分布式電源系統的負載有以下幾種基本類型:(1)恒功率負載:如變換器+電阻;(2)恒電阻負載:如常用的電阻;(3)恒流負載:如通過變換器給電池恒流充電;(4)恒壓負載:如通過變換器給電池恒壓充電。上述基本類型的負載可以組合為更為復雜的負載,這種組合可以是空間上的組合,如幾種不同類型負載的并聯;也可以是時間上的組合,如在一個時間段內是這種類型的負載,在下一個時間段內,則變為另一種類型的負載。
3 分布式電源系統中的非線性因素分析
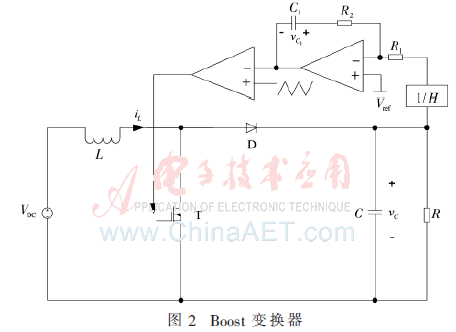
在分布式電源系統中,開關變換器是造成系統非線性的最主要因素,其次是分布式電源系統中有些源和負載本身是非線性的。開關變換器是非常復雜的非線性時變離散系統。開關器件周期性的導通與關斷使得開關變換器的主拓撲是一個時變電路。開關變換器又是一個離散系統,系統中既存在模擬量,又存在數字量。控制電路中的脈寬調制器將連續的模擬量轉換為離散的開關序列(數字量),用以驅動開關器件的導通和關斷。同時,開關變換器是復雜的非線性系統,下面結合圖2所示的Boost電路對此進行分析。
3.1 占空比恒定時主拓撲電路結構切換造成的非線性
主拓撲中開關器件的導通與關斷會引起電路結構的改變。多個開關器件導通與關斷的不同組合形成不同的電路結構。開關變換器中的開關器件主要有3種類型,第一種是以MOSFET、IGBT為代表的全控型器件,第二種是以二極管為代表的不控型器件,另外還有以晶閘管為代表的半控型器件。我們重點考慮在DC-DC變換器中使用的前兩種類型的開關器件。全控型器件的通斷由主拓撲外部的控制電路來進行驅動,不控型器件的通斷則由主拓撲電路自身的結構和狀態來決定。當圖2所示的Boost變換器工作在CCM模式時,不控型器件二極管的開關狀態與全控型器件的MOSFET形成互補,主拓撲有兩種可能的電路結構;Boost變換器工作在DCM模式時,當MOSFET關斷后,若電感電流不為0,二極管導通,若電感電流為0,二極管斷開,所以DCM下Boost電路有3種可能的電路結構。
占空比恒定時,變換器工作在穩態或者開環模式。在一個開關周期內,不同的電路結構所占時間的比例是不變的。主拓撲中的每一種電路結構,單獨來看都是線性的,但不同的電路結構,電源是否接入電路、電容的充放電狀態、電感電流的增減狀態都不太一樣,隨著開關器件的導通與關斷,開關變換器也在不同的電路結構間切換,從而造成了主拓撲電路的非線性,電流、電壓等在電路結構切換時,發生非線性變化,形成開關紋波。
3.2 變化占空比造成的非線性
若忽略掉開關紋波的影響,既然每一種電路結構都是線性的,那么主拓撲電路是否就是線性的了呢?要回答這個問題,我們先來建立變換器的大信號狀態平均模型。
由于開關紋波幅值很小,一般遠小于平均值,可以近似認為狀態變量的平均值與瞬時值相等,而不會引起較大的誤差。對于CCM模式下的變換器,有兩種可能的電路結構。設源為直流電壓源,負載為阻值不變的電阻負載,開關周期為Ts,占空比為d。在每個開關周期的[0,dTs]時間段內,主拓撲為一種電路結構,設狀態方程為:

式中:A1,B1,C1,D1為系數矩陣;u為系統輸入;y為系統輸出;x為系統的狀態變量。
在每個開關周期的[dTs,Ts]時間段內,主拓撲為另一種電路結構,設狀態方程為:

式中:A2,B2,C2,D2為系數矩陣。
根據狀態平均的原理,最終的狀態平均方程為:
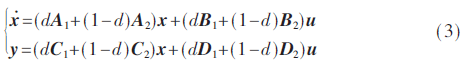
若變換器工作在開環狀態,占空比d可看成一個像電感、電容一樣的固定不變的參數,則由式(3)可以看出,狀態平均方程是線性的。但在閉環情況下,變換器的占空比是變化的,通常是電感電流和電容電壓的函數,設d=f(x),在狀態方程中,會出現d·x=f(x)·x或d·u=f(x)·u,即會出現兩個狀態變量相乘或者狀態變量與輸入相乘的非線性乘積項。類似地,可建立DCM下Boost電路的狀態方程模型,DCM下Boost電路的狀態方程要復雜些,因為電感電流存在斷續的狀態。但同樣地,狀態方程中也會出現兩個狀態變量相乘或者狀態變量與輸入相乘的非線性乘積項。由此可見,使用狀態平均方法消除了狀態變量中由開關動作引起的紋波和由此帶來的非線性,把時變系統轉變為時不變系統,但狀態方程中仍然含有非線性因素。這種非線性在狀態方程中體現為狀態變量相乘或狀態變量與輸入相乘的非線性乘積項;在由受控源替代開關元件的等效電路中體現為受控源的表達式為非線性乘積項;在物理意義上體現為在一個開關周期內,不同的電路結構所占時間的比例不是恒定不變或線性的,而是受狀態變量控制的非線性表達式。在使用狀態平均法建立小信號模型時,正是忽略了這些非線性乘積項,才使得小信號模型成為線性模型。
3.3 控制電路中的非線性
控制電路中的非線性主要是由飽和現象造成的,包含以下兩個方面:一是控制器的輸出電壓被供電電壓所鉗制,在電壓模式的PWM控制器和電流模式的PWM控制器中會存在這樣的飽和現象;二是占空比被限制在0到1之間,這樣的占空比限制存在于任何一個開關變換中,實際工程中占空比的最小值和最大值可能不是0和1,而是介于0到1之間的值。
3.4 源和負載的非線性
在分布式電源系統中,開關變換器的源和負載的非線性體現在以下兩個方面。一方面是變換器的源和負載本身帶有非線性。如源是蓄電池組、太陽電池陣等,其U-I特性曲線都呈現非線性特征。又如負載可能是電機、時斷時續的加熱器或者功率在某個范圍內變化的變功率負載[7]等非線性負載。另一方面是變換器引起的非線性。在分布式電源系統中,存在級聯、并聯、串聯等情況,很多時候變換器不是直接和源、負載相連接,中間可能經過多個變換器,變換器的“源”和“負載”可能是其他變換器和源、其他變換器和負載的組合,這種組合常常呈現非線性特性。如兩個開關變換器級聯時,后級變換器和電阻負載作為前級變換器的“負載”,其負載特性可以看作恒功率負載,電阻負載是線性的,恒功率負載卻是非線性的,而且,恒功率負載是對該負載特性的一種近似表示,真實的后級變換器和電阻負載的非線性特性要復雜得多。
3.5 器件的非線性
電感、電容在通過不同的電流、電壓時,其電感值、電容值可能發生變化,比較典型的是電感會有飽和現象。另外,器件的特性也會受溫度和老化的影響而發生變化。器件的這些特性變化中含有非線性因素。
4 結論
分布式電源系統中包含開關變換器等非線性模塊,模塊間存在級聯、并聯、源分立、負載分立等多種連接方式,使用線性理論的方法很難準確分析分布式電源系統的特性,這使得分布式電源系統的設計和分析都比較復雜,同時也容易引起系統的不穩定問題。本文介紹了分布式電源系統的建模方法,并對分布式電源系統可能存在的非線性影響因素做了全面分析,總結了5種造成分布式電源系統非線性的因素,為進一步使用非線性方法分析分布式電源系統的特性奠定了基礎。
參考文獻
[1] SURANYI G G.The Value of Distributed Power[C].IEEE Proceedings of Applied Power Electronics Conference and Exposition,1995:104-110.
[2] LUO S.A review of distributed power systems part I-DC distributed power system[J].Aerospace and Electronic Systems Magazine,2005,20(8):5-16.
[3] 李安壽,張東來,楊煬.開關變換器的穩定性定義及分析方法[J].電力電子技術,2013,47(11):27-29.
[4] LIUTANAKUL P,AWAN A,PIERFEDERICI S,et al.Linear stabilization of a DC bus supplying a constant power load[J].IEEE Transaction on Power Electronics,2010,25(2):475-488.
[5] Zhang Fanghua,Yan Yangguang.Start-up process and step response of a DC-DC converter loaded by constant power loads[J].IEEE Transactions on Industrial Electronics,2011,58(1):298-304.
[6] KNYAZKIN V,CANIZARES C A,S?魻DER L H.On the parameter estimation and modeling of aggregate power system loads[J].IEEE Transactions on Power Systems,2004,19(2):1023-1031.
[7] 劉青.快速參考跟蹤電源的研究[D].哈爾濱:哈爾濱工業大學,2013.

