劉笑辰，朱磊，夏蘇

　　（ 解放軍理工大學 通信工程學院，江蘇 南京 210007）

　　摘要：在現實生活中，許多大型的通信網絡或電力網絡都可以應用復雜網絡進行刻畫。然而網絡中某些“關鍵節點”一旦遭到攻擊極易引發相繼故障。這種現象的存在極大降低了網絡的可靠性。為了提高網絡對相繼故障的抵御能力，針對現有基于最短路徑的路由算法加以改進，降低“關鍵節點”在網絡中所起的作用，提高了網絡負載在各節點間分布的均衡性。通過在典型的復雜網絡上進行的仿真實驗，證明了改進的路由算法能夠大大增強網絡對相繼故障的抵御能力。

　　關鍵詞：復雜網絡；相繼故障；路由算法；網絡可靠性

0引言

　　現實生活中的諸多網絡比如電力網、通信網、交通網以及社交網等都可以用復雜網絡模型進行描述。Albert等人提出復雜網絡中的相繼故障現象［1］，即網絡中極少數所謂的“關鍵節點”遭到破壞將引起連鎖反應，導致整個網絡呈現雪崩式毀壞。相繼故障的存在對社會生活的正常運行構成了極大的威脅。

　　為了減少相繼故障的危害，提高網絡的可靠性，許多學者進行了卓有成效的研究。參考文獻［2］按照一定的規則在網絡中選擇某些節點執行一次防御策略，如果被保護的節點負載超過閾值則將額外的負載分配給鄰居從而避免本身發生故障。參考文獻［3-5］注重在網絡中發現在相繼故障過程中更加重要的節點。由于在現實中，往往多個網絡相互作用形成一個耦合的整體，參考文獻［6-7］在耦合網絡中挖掘重要組成部分并且設計出負載分配策略。

　　在當前復雜網絡相繼故障的防御策略研究中，大多數學者著眼于發現網絡中起到關鍵作用的節點或組成部分，而缺少對網絡中路由算法的改進以提高網絡的可靠性。本文通過對現有基于最短路徑的路由算法加以改進，將網絡拓撲結構的影響體現到傳輸鏈路的效率中，降低復雜網絡中節點負載的異質性，進而提高網絡對相繼故障的抵御能力。

1基于最短路徑路由算法的改進研究

　　在計算網絡中的源節點到目的節點最短路徑的過程中，節點間鏈路的傳輸耗費是一個關鍵的參數。本文通過對節點間傳輸的實際耗費進行修正得到虛擬耗費，然后根據虛擬耗費計算節點之間的最短路徑。通過虛擬耗費的計算降低經過度數大的節點的路徑數目，從而降低這些節點的負載，進而減少各節點負載之間的異質性使得網絡更加健壯。

　　1.1算法的基本思想

　　令網絡G中各節點之間的鄰接矩陣為A，其中aij為其中的一個元素，并有：

　　其中eij表示節點i與j之間的連邊。

　　假設網絡中的節點數為n，存在實際耗費因子向量Cr=(λr1,λr2,λr3…λrn)表示各節點對相鄰的邊傳輸實際耗費的影響，其中λri為節點i的實際耗費因子，根據節點的實際耗費因子可得邊eij傳輸的實際耗費為：

　　crij=λri·λrj·aij(2)

　　考慮到復雜網絡中各節點間度數分布的異質性，為了防止網絡中度數大的節點承擔過多的負載，根據節點的度數對其實際耗費因子進行修正得到節點的虛擬耗費因子。令節點i的虛擬耗費因子為：

　　λvi=f(λri,ki)(3)

　　式(3)的計算將在下節中討論。根據式(3)可以得到虛擬耗費因子向量Cr=(λv1,λv2,λv3…λvn)，從而得到eij的虛擬耗費：

　　cvij=λvi·λvj·aij(4)

　　根據網絡的虛擬耗費矩陣計算各節點之間傳輸的最短路徑，可以采用Floyd、BellmanFord、SPFA等算法［8］得到網絡間節點傳輸的路由表。運用上述方法得到的結果可以有效降低網絡中度數大的節點的負載，提高各節點間負載的均衡性。

　　1.2節點虛擬耗費因子的計算

　　節點的虛擬耗費因子由該點的度數和實際耗費因子決定。在計算節點度的影響時做出如下假設：

　　(1)假設每個節點存在虛擬負載，節點i的負載為lvi  = logk ki，其中ki為節點i的度數，k表示網絡中節點的平均度。

　　(2)每個節點在單位時間內可以處理的負載與該節點的度數成正比，并且其比例系數與節點的虛擬負載成反比。

　　(3)整個網絡在單位時間內能夠處理掉所有節點中的虛擬負載。

　　對于假設(1)，由于在一個完好的網絡中不存在孤立的節點，即所有節點的度數都大于等于1，故虛擬負載lvi可以保證有意義；對于假設(2) ，考慮度數大的節點能夠與更多的節點進行交流并且算法的最終目的在于均衡節點間的虛擬耗費因子，由上述假設可以得到以下方程組：

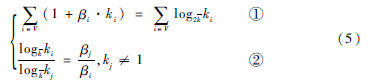
　　方程①的左側表示所有節點單位時間內處理的虛擬負載，其中1表示負載傳遞給節點本身，βi·ki表示負載傳遞給周圍的鄰居；方程的右側表示網絡中所有節點的虛擬負載之和。并有當kj=0時所對應的βj=0。

　　計算方程(5)可以得到：

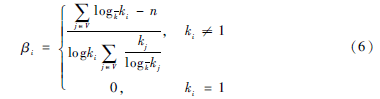
　　對于節點i而言，最終該點的虛擬耗費因子為：

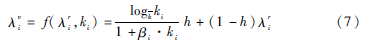
　　其中h是一個可調參數，該值越大則算法對關鍵節點作用的削弱就越大。

　　圖1表示了在初始實際耗費因子向量Cr(0)=(1,1,1,…,1)時3個不同的無標度網絡中節點的虛擬耗費因子與度數的關系。網絡1中初始節點個數為7，每次新增加的節點連邊數為3，算法中h=0.2。網絡2中初始節點個數為8，每次新增加的節點連邊數為6，算法中h=0.2 。網絡3中初始節點個數為8，每次新增加的節點連邊數為6，算法中h=0.6。從圖中可以看出，在各節點實際耗費因子相同的情況下，節點的度數越大其虛擬耗費因子就越大。通過網絡2與網絡3的對比可以發現，參數h增大，擬合曲線的斜率也相應增大。　

2實驗仿真及結果研究

　　在仿真實驗中，本文分別在BA無標度網絡［1］及WS小世界網絡［9］中對改進的路由算法的效果進行研究。本文應用參考文獻［10］中的相繼故障模型，并且令對任意節點i均有λri(0)=1。文中采用平均傳輸效率E(G)衡量網絡狀態 ［11］。E(G)越大表示網絡在單位時間內傳輸能力越強，即網絡狀態越好。

　　圖2是3種不同的無標度網絡發生相繼故障后網絡的效率變化。圖中網絡1表示應用基于最短路徑路由算法的網絡，網絡2表示應用改進路由算法的網絡。橫坐標表示初始時刻網絡中負載最大的前n個節點發生故障，縱坐標表示網絡的平均傳輸效率。圖2無標度網絡發生相繼故障后平均傳輸效率的變化

　　圖(a)、(b)、(c)中的網絡初始節點數分別為4、6、8，每個新增加節點的連邊數為3、5、6。各網絡的節點總數均為1 000。實驗選取網絡中初始負載最大的若干個節點使之發生故障，并記錄發生相繼故障后經過30個時間單位后網絡的平均傳輸效率E(G)。結果表明，隨著初始故障節點的增多，網絡的平均傳輸效率都會降低。但是在采用傳統的路由算法的網絡中，網絡平均效率下降的速度非常快并且在3種情況下最終都接近于0，即網絡已經完全崩潰。在應用改進后的路由算法的網絡中，盡管網絡的效率也發生了下降，但相比而言其下降速率非常緩慢，根據圖2(b)、(c)，在已有15個節點發生故障的情況下，網絡仍然保持著相當程度的平均效率，而與其相對的傳統網絡已經完全崩潰。在圖2中，采用改進路由算法的網絡的初始平均傳輸效率要略小于傳統的網絡，但其結果卻大大增強了網絡對相繼故障的抵抗能力。

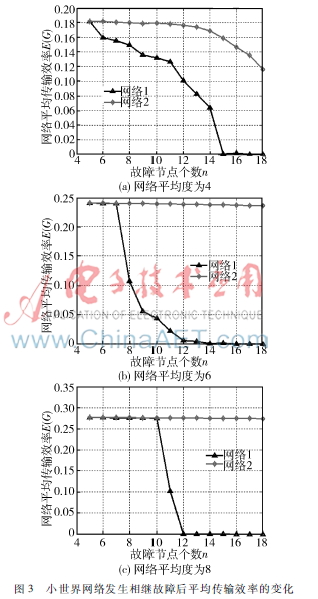
　　圖3記錄了3種不同的小世界網絡發生相繼故障后的變化。圖中網絡1表示應用基于最短路徑路由算法的網絡，網絡2表示應用改進路由算法的網絡。圖(a)、(b)、(c)中網絡的平均度分別為4、6、8。各網絡隨機連邊的效率為0.4，節點總數均為1 000。實驗同樣使網絡中初始負載最大的一些節點發生故障。結果顯示在WS網絡中，改進的路由算法能夠明顯增強網絡對相繼故障的抵御能力。在應用改進路由算法的網絡中，數目較少的故障節點對網絡造成的危害非常輕微。在圖3(b)、(c)中可以看出，當小世界網絡的平均度數增大時，應用改進路由算法的網絡具有更強健壯性。

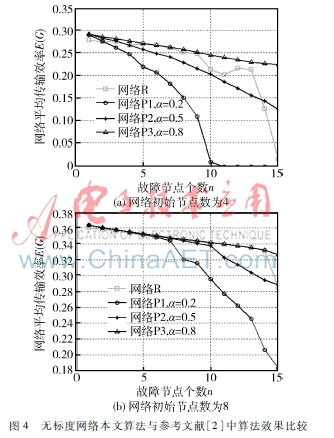
　　在無標度網絡中將本文提出的路由改進算法與參考文獻［2］中提供的方法進行比較，兩種策略增強網絡抵御相繼故障能力的效果如圖4所示。圖中的數據均為網絡發生相繼故障后的結果。圖中網絡R表示應用本文改進路由算法的網絡；網絡P表示應用參考文獻［2］中增強網絡健壯性方法的網絡，其中α表示網絡中采用防御策略的節點占總節點的比例。圖4(a)、(b)中的網絡初始節點數分別為4、8，每個新增加節點的連邊數為3、6。各網絡的節點總數均為1 000。

　　從圖4可以看出，在網絡中初始故障節點較少時，本文提出的算法與參考文獻［2］中80%的節點采取保護措施所達到的效果相當。但是本文改進的算法并不需要對網絡中的節點提出特殊的要求，從經濟的角度來講本文算法更優。值得注意的是，隨著網絡中故障節點的增多，應用本文所提算法的網絡對相繼故障抵抗能力下降較快，其在這一點上表現不如參考文獻［2］中的策略。

　　在小世界網絡中將本文提出的路由改進算法與參考文獻［2］中提供的方法進行比較，圖5記錄了兩種策略增強網絡抵御相繼故障能力的效果。圖中的數據均為網絡發生相繼故障后的結果。網絡R表示應用本文改進路由算圖5小世界網絡中本文算法與參考文獻［2］算法比較法的網絡；網絡P表示應用參考文獻［2］中增強網絡健壯性方法的網絡，α表示網絡中采用防御策略的節點占總節點的比例。圖5(a)、(b)中的網絡的平均度分別為4、6。各網絡隨機連邊的概率為0.4，網絡中的節點總數為1 000。從圖中可以看出在小世界網絡中與參考文獻［2］中的方法比較，本文所提出的改進路由策略同樣能得到良好的效果。

3結論

　　在復雜網絡中存在若干“關鍵節點”，這些節點對網絡的正常運行發揮著重要的作用。然而一旦這些節點遭受攻擊則極易引發相繼故障。為了減少相繼故障的發生，提高網絡的可靠性，本文對現有的路由算法加以改進。通過降低網絡中度數大的節點的重要性，使得網絡中各節點的負載分布更加均衡，從而減少了“關鍵節點”在網絡中發揮的作用，進而增強了網絡對蓄意攻擊的抵御性能。通過在BA無標度網絡及WS小世界網絡中進行的實驗，驗證了在故障節點數不多的情況下改進的路由算法能夠大大提高網絡對相繼故障的抵御能力。但是當網絡中初始故障節點數增多時改進路由算法的效果下降比較明顯，同時由于改進路由算法的應用，致使網絡的初始傳輸效率有所降低，這也體現了網絡的可靠性與有效性之間的辯證關系。

參考文獻

　　［1］ BARABAI A L, ALBERT R. Emergence of scaling in random networks［J］. Science, 1999, 286（5439）: 509512.

　　［2］ WANG J. Mitigation strategies on scalefree networks against cascading failures［J］. Physica A: Statistical Mechanics and Its Applications, 2013, 392（9）:22572264.

　　［3］ CHEN D, LV L， SHANG M S， et al. Identifying influential nodes in complex networks［J］. Physica A: Statistical Mechanics and Its Applications,2012, 391(4): 17771787.

　　［4］ 任卓明, 邵鳳, 劉建國, 等. 基于度與集聚系數的網絡節點重要性度量方法研究［J］. 物理學報, 2013（12）:522526.

　　［5］ ZHANG X, ZHU J, WANG Q, et al. Identifying influential nodes in complex networks with community structure［J］. KnowledgeBased Systems, 2013, 42(2): 7484.

　　［6］ SCHNEIDER C M, YAZDANI N, ARAU＇JO N A, et al. Towards designing robust coupled networks［J］. Scientific Reports, 2011，3(24)： 17.

　　［7］ BRUMMITT C D, D’SOUZA R M, LEICHT E A. Suppressing cascades of load in interdependent networks［J］. Proceedings of the National Academy of Sciences, 2012, 109(12):680689.

　　［8］ ALBERTO L G, INDRA W. Communication networks: fundamental concepts and key architectures［M］. New York: Mc GrawHill, 2000.

　　［9］ WATTS D J, STROGATZ S H. Collective dynamics of ‘smallworld’networks［J］. Nature, 1998(393):440442.

　　［10］ MOTTER A E, LAI Y C. Cascadebased attacks on complex networks［J］. Physical Review E, 2002, 66(6):114129.