0 引言

　　近年來無線傳感器網絡（Wireless Sensor Network，WSN）在很多領域得到了廣泛的應用，如目標的定位與跟蹤和動物行為監控等。而精確的目標位置信息是上述應用的基礎，因此，無線傳感器網絡的定位技術一直是研究的熱點。基于距離的定位算法可利用到達時間（TOA）、到達時間差（TDOA）和到達角度（Angle of Arrive，AOA）等測量值，實現對目標的定位。其中，AOA的測量精度高于TOA和TDOA，基于AOA的定位算法不需要各傳感器之間進行時鐘同步[1，2]，但是AOA測量設備的尺寸和成本限制了它的應用，然而信號處理技術和設備制造技術的發展很好地解決了上述問題，所以近年來基于AOA的定位算法又得到了關注。

　　關于基于AOA的定位算法，相關學者已經做了很多研究。文獻[1-3]利用錨節點與目標的方位線兩兩之間的交點進行加權求和估計目標的位置，這類算法可稱為基于權值交點的AOA定位算法。文獻[3]提出了CAOA算法，該算法將所有的方位線交點的均值作為目標的估計位置。文獻[4，5]提出了SA算法，利用方位線交點的閉式解的一階或二階偏導定義各交點的敏感度，生成相應的權值，再進行加權求和。文獻[1，2]在定位誤差分析的基礎上提出了基于權值方位線交點的定位算法。文獻[1]提出WIAOA算法利用錨節點之間的距離、錨節點與目標的AOA測量值及其標準差構建方位線交點的權值。文獻[2]提出的CWIAOA定位算法利用方位線交點的CRLB值得到交點的權值。而某些交點雖具有較大的權值，但其與目標真實位置之間的偏差卻比權值較小的交點的偏差大，將這樣的交點用于目標位置的估計會嚴重影響估計的精度，這樣的交點可稱為奇異方位線交點。

　　本文給出了一種基于GDOP(Geometric Dilution of Precision)權值交點的魯棒AOA定位（RGWIAOA）算法，該算法利用圓誤差概率剔除奇異方位線交點，將剩余的方位線交點視為有效交點，對有效交點賦予相應的歸一化權值并進行加權求和，完成對目標的位置估計。算法只對有效交點進行加權求和，同時在權值的計算中考慮了錨節點的位置誤差，使算法有較高的定位精度，并且在不同的應用環境下具有較好的魯棒性。

1 模型的建立

　　AOA算法利用錨節點測量盲節點信號的達到角度，建立錨節點與盲節點之間的方位線，兩條方位線的交點即為盲節點位置的粗估計值。這里假設各錨節點與盲節點之間不存在遮擋，即信號傳播存在直達徑，錨節點能測量定位信號的AOA。

　　假設有N個位置已知但存在誤差的固定錨節點，和分別表示第i個錨節點的已知位置和真實位置，nxi為xi與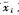之間的誤差，nyi為yi與之間的誤差，nxi和nyi均服從零均值的正態分布，標準差分別為?滓xi和?滓yi，。表示第i個錨節點AOA的測量值，表示第i個錨節點AOA的真實值，ni表示第i個錨節點AOA測量值的誤差，其服從均值為零且標準差為?滓i的正態分布。盲節點的位置是未知的，用p=(xT，yT)表示其真實位置。算法對盲節點位置的估計結果用表示。定位模型可以用如下公式表示：

　　其中，

2 基于GDOP權值交點的魯棒AOA定位算法

　　基于權值交點的AOA定位算法的核心思想是，在獲得所有連接錨節點和盲節點的方位線間的兩兩交點的基礎上，對交點進行加權求和，作為目標位置的估計值，其一般公式為：

　　式中，N為錨節點的個數，和分別為方位線交點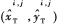在x軸和y軸上的歸一化權值，不同算法的區別在于和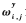的確定過程。

　　為提高基于權值交點的AOA定位算法的定位精度，首先應剔除那些權值較高但偏離盲節點實際位置距離較大的方位線交點。為此可以考慮引入圓誤差概率解決這個問題。二維環境下圓概率誤差的定義為定位結果落到以錨節點真實位置為中心的圓形區域C的概率。圓形區域C這里稱為誤差概率圓，它的半徑定義為幾何精度因子半徑的n倍[6]，由式(5)確定，其中RCEP-P表示定位結果以概率P落入圓形區域C的半徑。根據文獻[6]，式(5)中P與n的關系可由式(6)確定，通過推導得到式(7)。

　　圓形區域C的圓心為盲節點的真實位置，而對于定位問題，盲節點的位置是未知的。這里以方位線的交點代替盲節點的真實位置(xT，yT)，其誤差概率圓的半徑可由下式得到：

　　其中，代表方位線i和方位線j的交點的誤差概率圓的半徑。N條方位線共有個交點，若方位線交點與之間的距離滿足：

　　則認為和為有效交點。在概率為P條件下，找出有效交點，將有效交點用于盲節點的位置估計，從而減小奇異方位線交點對定位精度的影響。

　　下面討論GDOP的計算問題。在考慮錨節點的位置存在誤差的情況下，根據式（3）對求微分，得：

　　其中：

　　令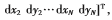，且：

　　得：

　　利用偽逆求解盲節點定位誤差估計值為：

　　假設各錨節點的AOA測量誤差互不相關，且錨節點位置誤差各元素之間及各錨節點位置誤差也互不相關，故：

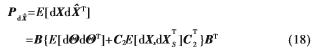
　　式中，

　　上述GDOP的計算方法，既考慮了錨節點的AOA測量誤差，也考慮了錨節點位置的誤差，具有較強的適應性。這里仍然以方位線i和方位線j的交點代替盲節點的真實位置，得到：

　　綜上，方位線i和j的交點，在x軸和y軸上的非歸一化的權值為：

　　式中，和分別代表矩陣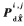的主對角線上的兩個元素。所有有效方位線交點構成的集合為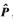，令：

　　若方位線交點不屬于，則：

　　若方位線交點屬于，則其歸一化權值表示為：

　　根據式(22)、式(23)，對各方位線交點進行加權求和，盲節點位置的估計值為：

　　綜上所述，本文所給的基于GDOP權值交點的魯棒AOA定位算法主要包括以下三步：(1)錨節點獲得AOA測量值；(2)得到方位線交點，確定有效交點；(3)有效交點加權求和，估計目標位置。RGWIAOA算法的具體步驟如下：

　　初始化：錨節點(xi，yi)或，i=1，2，…，N，AOA測量值，圓誤差概率P=0.5，有效交點個數門限。

　　算法過程：盲節點(xT，yT)定位。

　　(1)獲得方位線交點；

　　(2)分別根據式(19)計算GDOPi，j；

　　(3)分別根據式(8)計算；

　　(4)計算方位線交點之間的距離，根據式(23)確定有效交點集合；

　　(5)若有效交點個數小于，則加大圓誤差概率P并重復步驟(3)；

　　(6)根據式(20～２３)計算各方位線交點的權值；

　　(7)根據式(24)估計盲節點的位置。

3 仿真結果與分析

　　為驗證本文所給算法的性能，本節在幾種典型場景下對RGWIAOA算法、CAOA算法、WIAOA算法、CWIAOA算法和SA算法的定位性能進行比較。在每個場景下，每種算法進行1 000次Monte-Carlo仿真，統計算法的均方根誤差。

　　(1)場景1：6個錨節點沿半徑為60 m的圓形邊緣均勻分布，錨節點位置分別為（120，0）、（90，51.96）、（30，

　　51.96）、（0，0）、（30，-51.96）和（90，-51.96），且錨節點的已知位置與真實位置相比不存在誤差，盲節點位置為（60，0）。各錨節點對盲節點的AOA測量值的誤差互不相關，且的取值范圍為[1°，5°]。

　　圖1為場景1下各算法的RMSE隨?滓?茲變化的曲線。從圖 1中可以看出在場景1下，CAOA算法的性能最差，其RMSE偏離CRLB較遠，其他算法性能接近，且它們的RMSE基本達到CRLB。

　　(2)場景2： 6個錨節點沿直線等間距分布，間距為20 m，錨節點位置分別為（-50，0）、（-30，0）、（-10，0）、（10，0）、（30，0）和（50，0），且錨節點的已知位置與真實位置相比不存在誤差，盲節點位置為（0，60）。各錨節點AOA測量值的誤差互不相關，且取值范圍為[1°，5°]。

　　圖2為場景2下各算法的RMSE隨變化的曲線。從圖 2中可以看出在場景2下，CAOA算法的性能最差，其RMSE偏離CRLB的程度隨的增加而增大，RGWIAOA算法的整體性能優于其他算法，但當>4°時RGWIAOA算法的RMSE與CRLB有較小的偏離。

　　對比場景1和場景2，可以發現上述幾種算法的定位性能在場景1下比在場景2下要好，即錨節點分布盲節點的周圍時，算法的定位性能比較好。

　　(3)場景3：錨節點位置誤差各元素之間及各錨節點位置誤差也互不相關，且其他條件與場景2一致。

　　圖3為場景3下各算法的RMSE隨?滓?茲變化的曲線。從圖 3中可以看出在場景3下，CAOA算法的性能最差，其RMSE偏離CRLB的程度隨?滓?茲的增加而增大，RGWIAOA算法的整體性能優于其他算法。但由于錨節點的已知位置存在誤差，將其用于位置解算，故上述5種算法的RMSE與CRLB相比均會存在一定的偏差。對比圖 3和圖 2還可以發現，在一定的情況下，對算法性能的影響會隨著增大而相對減弱。

　　綜上所述，仿真結果表明，本文所給RGWIAOA算法在不同場景下，較其他幾種算法有更好的適應性，且該算法的定位精度在整體上優于其他算法。

4 結束語

　　本文給出了一種基于GDOP權值交點的魯棒AOA定位算法。算法的核心思想是在所有方位線交點的基礎上利用圓誤差概率確定有效交點，根據有效交點的GDOP為其賦予相應的權值，并對有效交點進行加權求和，得到目標的位置估計。RGWIAOA算法充分利用了錨節點AOA測量值的標準差，同時在GDOP的計算中考慮了錨節點自身位置的誤差對計算結果的影響。仿真結果表明，RGWIAOA算法與WIAOA算法、CWIAOA算法、SA算法和CAOA算法相比，具有更好的適應性，且算法的整體定位精度更高。

　　參考文獻

　　[1] ZHOU Q，DUAN Z.Weighted intersections of bearing lines for AOA based localization[C].Information Fusion (FUSION2014)，2014 17th International Conference on.University of Salamance：IEEE，2014：1-8.

　　[2] DUAN Z，ZHOU Q.CRLB-weighted intersection method for target localization using AOA measurements[C].Computational Intelligence and Virtual Environments for Measurement Systems and Applications(CIVEMSA)，2015 IEEE International Conference on，Shenzhen China：IEEE，2015：141-146.

　　[3] BRIDA P，MACHAJ J，BENIKOVSKY J，et al.A new complex angle of arrival location method for ad hoc networks[C].Proceedings of the 7th Workshop on Positioning Navigation and Communication(WPNC 07)，Dresden Germany：IEEE，2010：284-290.

　　[4] SOLTANIAN M，PEZESHK A M，MAHDAYI A，et al.A new iterative position finding algorithm based on taylor series expansion[C].Electrical Engineering(ICEE)，2011 19th Iranian Conference on，IEEE，2011：1-4.

　　[5] PEZESHK A A M，DALLAI M.A novel method for position finding of stationary targets using bearing measurements[C].Proceedings of the C4I Conference at Sharif University of Technology，2010.

　　[6] YU K G，SHARP I，GUO J Y.Ground-based wireless positioning[M].Chichester：Wiley-IEEE Press，2009.