文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.172555
中文引用格式: 周應超,黃瓊,申濱. 基于內波束干擾消除的大規模MIMO低復雜度波束成形[J].電子技術應用,2017,43(8):16-20.
英文引用格式: Zhou Yingchao,Huang Qiong,Shen Bin. Low-complexity beamforming based on inter-beam interference cancellation for massive MIMO[J].Application of Electronic Technique,2017,43(8):16-20.
0 引言
在最近幾年時間里,大規模MIMO技術得到了廣泛的重視與研究,并被認為是第五代移動通信系統中的關鍵技術之一[1-3]。大規模MIMO的主要優點體現在降低發射功率、提升能量效率并采用多址接入和復用增益大幅提升頻譜效率[4]。大規模MIMO系統利用其提供的空間自由度能在不增加時頻資源的情況下在同一時頻資源上向多個用戶發送信號[5],其波束成形技術能有效抑制多址干擾,是其物理層中的關鍵技術之一,其中研究較多的傳統波束成形,如最小均方誤差(Minimun Mean Square Error,MMSE)[6-7]波束成形和奇異值分解(Singular-Value Decomposition,SVD)[8-9]波束成形,因其帶來的高計算復雜度,限制了其在實際中的應用。在商業無線網絡中降低部署大規模MIMO系統時的實施復雜度是非常值得關注的,最大比傳輸(Maximum Ratio Transmission,MRT)[10]波束成形和迫零波束成形(Zero-Forcing beamforming,ZFBF)[11-12]因實施較簡單,被廣泛應用于大規模MIMO系統。其中MRT復雜度最低,是實施起來最簡單的波束成形算法,但其缺點為存在用戶間干擾,和速率性能明顯劣于其他波束成形技術,即使利用合適的用戶選擇技術也難以避免用戶間干擾的問題。ZFBF則可以完全消除用戶間的內波束干擾,提供較高的和速率性能,但其計算復雜度較MRT也高出許多。利用迭代QR分解(QRD)計算ZFBF的波束成形矩陣能降低其計算復雜度[12],然而文獻[12]中的QRD考慮的場景是用戶端全復用情況下能降低ZFBF的計算復雜度。當用戶端不是進行全復用時,QRD則需要額外的運算操作,從而進一步增大其計算復雜度。因此在大規模MIMO系統中,當用戶端復用不全時,基于QRD的ZFBF要求的計算復雜度會高于傳統ZFBF。
本文提出一種基于部分內波束干擾消除的低復雜度BF算法,考慮消除部分用戶間的內波束干擾,以此來實現計算復雜度與和速率性能之間的良好折衷。假定用戶間的內波束干擾大小不相等,為了降低計算復雜度,考慮只消除一些數值大的內波束干擾。為此,首先通過傳統MRT技術生成用戶的波束成形矢量,然后計算用戶間內波束干擾量,再通過內波束干擾消除算法的一系列矢量運算,去除一部分干擾量大的強干擾,以此避開復雜的高維度矩陣運算和矩陣求逆,因而能達到計算復雜度與和速率間的良好折衷。
1 大規模MIMO系統模型
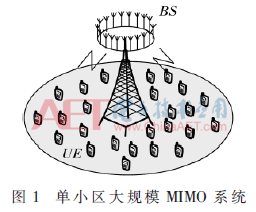
圖1所示為大規模MIMO的下行鏈路,基站端部署了N根天線,可在同一時頻資源中與用戶集ΩM中的M個單天線用戶通信,且N≥M。假設環境模式是時分雙工(Time Division Duplex,TDD)模式,信道衰落為平坦瑞利衰落,基站端天線可以獲得完整的信道狀態信息(Channel State Information,CSI)。


2 內波束干擾消除算法
傳統波束成形技術,如文獻[6,7]和文獻[8,9]中的MMSE和SVD發送信號時,其和速率性能接近最優波束成形,但其計算復雜度過高,都不便于在實際中實施。因此,為了大幅度降低計算復雜度同時保持和速率損失較小,本節提出了基于部分內波束干擾消除的低復雜度BF算法。
發端利用MMSE目的是最小化發送符號與接收符號的均方誤差(Mean Square Error,MSE):

2.1 算法設計
傳統波束成形技術,如文獻[10]中的MRT和文獻[11,12]中的ZFBF,因其便于實際中的實施和良好的和速率性能,被廣泛應用于多用戶信號傳輸。MRT和ZFBF的波束成形矩陣表達式如下:

且提供較優的和速率,但其計算復雜度較高,在大規模MIMO環境中較難實施。文獻[12]中提出利用QRD可以降低ZFBF的復雜度,但當用戶端不是進行全復用時,基于QRD的ZFBF需要增加額外的運算操作,產生的復雜度會高于傳統ZFBF。
為便于實際中應用波束成形技術,考慮降低多用戶波束成形的計算復雜度,同時顯著降低來自其他用戶對目標用戶的內波束干擾,以此達到大幅度提高和速率的目的。考慮MRT場景下確定的波束矢量w,其會受到其他用戶的干擾。為了緩解其他用戶對目標用戶的內波束干擾,提高和速率性能,同時考慮實現的復雜性,本文采用內波束干擾消除算法,考慮消除每個用戶對其他M-1個用戶造成的內波束干擾中數值較大的S個強干擾,為平衡計算復雜度與和速率間的良好折衷,數值S可以預先確定。
來自用戶i對用戶k的內波束干擾量的大小為:


2.2 復雜度分析


3 仿真結果
通過仿真,驗證并比較了本文所提出的基于部分內波束干擾消除的低復雜度波束成形以及傳統波束成形的性能。
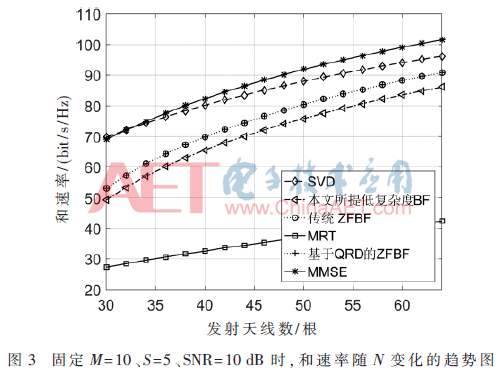
圖2和圖3描繪了當10個用戶信號以信噪比(SNR)為10 dB進行空間復用時,6種方案的和速率以及浮點計算數隨發射天線數變化的曲線,其中本文提出的基于部分內波束干擾消除的低復雜度BF算法的干擾消除數S為5。
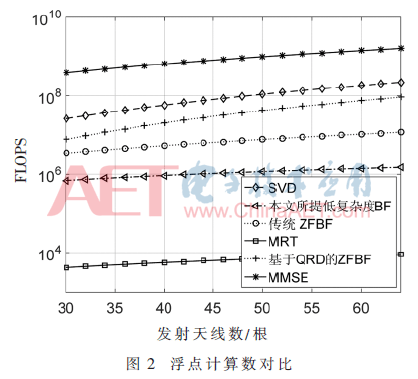
從圖2中可以看出,本文所提方案的浮點計算數要顯著低于MMSE、SVD、ZFBF等較優的傳統波束成形算法,且其曲線隨著發射天線數的增加更加趨于平緩;還可以看出基于QRD的ZFBF由于矩陣求逆運算和額外的組合運算,其浮點計算數要高于傳統ZFBF。
由圖3可見,本文所提方案的和速率性能接近于MMSE、SVD、ZFBF等較優的波束成形算法,遠高于MRT波束成形算法,且隨著基站天線數的增大,所提方案和速率逼近傳統ZFBF的和速率,可以實現ZFBF近90%的和速率,而只需要ZFBF的12%~19%的計算復雜度。
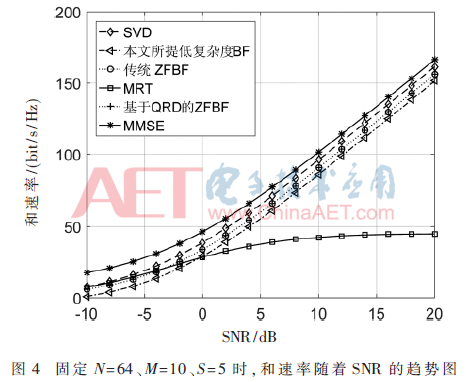
圖4描繪了本文所提方案以及5種傳統波束成形算法的和速率性能隨信噪比變化曲線比較圖(N=64、M=10、S=5)。由圖可知,本文所提低復雜度BF的和速率接近于MMSE、SVD、ZFBF等較優波束成形算法,遠大于MRT,并且隨著信噪比的增大,和速率性能逼近ZFBF。
4 總結
大規模MIMO系統中,傳統的波束成形算法,如MMSE、SVD、ZFBF等雖能提供較優的和速率性能,但是復雜度較高的高維矩陣求逆使其在現實實施中比較困難。MRT算法雖然復雜度最低,最易于實際應用,但是其和速率性能也是最差的。本文提出一種基于部分內波束干擾消除的低復雜度BF算法,首先在MRT場景下確立波束成形矩陣,再通過內波束干擾消除算法的一系列矢量運算生成新的波束成形矩陣,以此避開復雜度高的矩陣求逆操作。本文所提方案的計算復雜度較ZFBF得到了顯著降低,同時其和速率性能接近于ZFBF的和速率,遠大于MRT的和速率,所以此方案更適用于實際的應用。
參考文獻
[1] LARSSON E G,EDFORS O,TUFVESSON F,et al.Massive MIMO for next generation wireless systems[J].IEEE Communications Magazine,2014,52(2):186-195.
[2] MARZETTA T L.Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications,2010,9(11):3590-3600.
[3] RUSEK F,PERSSON D,LAU B K,et al.Scaling up MIMO:Opportunities and challenges with very large arrays[J].IEEE Signal Processing Magazine,2013,30(1):40-60.
[4] NGO H Q,LARSSON E G,MARZETTA T L.Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Transactions on Communications,2013,61(4):1436-1449.
[5] SHEN Z,CHEN R,ANDREWS J G,et al.Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization[J].IEEE Transactions on Signal Processing,2006,54(9):3658-3663.
[6] CHRISTENSEN S S,AGARWAL R,DE CARVALHO E,et al.Weighted sum-rate maximization using weighted MMSE for MIMO-BC beamforming design[J].IEEE Transactions on Wireless Communications,2008,7(12):4792-4799.
[7] SUN F,DE CARVALHO E.A leakage-based MMSE beamforming design for a MIMO interference channel[J].IEEE Signal Processing Letters,2012,19(6):368-371.
[8] ZHAN C Z,CHEN Y L,WU A Y.Iterative superlinear-convergence SVD beamforming algorithm and VLSI architecture for MIMO-OFDM systems[J].IEEE Transactions on Signal Processing,2012,60(6):3264-3277.
[9] SUDHIR A C,RAO B P.Implementation of wireless model for SVD based beam forming in MIMO systems[C].Devices,Circuits and Systems(ICDCS),2014 2nd International Conference on.IEEE,2014:1-6.
[10] PARFAIT T,KUANG Y,JERRY K.Performance analysis and comparison of ZF and MRT based downlink massive MIMOsystems[C].Ubiquitous and Future Networks (ICUFN),2014 Sixth International Conf on.IEEE,2014:383-388.
[11] CORVAJA R,ARMADA A G.Phase noise degradation in massive MIMO downlink with zero-forcing and maximum ratio transmission precoding[J].IEEE Transactions on Vehicular Technology,2016,65(10):8052-8059.
[12] LIU D,MA W,SHAO S,et al.Performance analysis of TDD reciprocity calibration for Massive MU-MIMO systems with ZF beamforming[J].IEEE Communications Letters,2016,20(1):113-116.
[13] CAIRE G,SHAMAI S.On the achievable throughput of a multiantenna Gaussian broadcast channel[J].IEEE Transactions on Information Theory,2003,49(7):1691-1706.
作者信息:
周應超,黃 瓊,申 濱
(重慶郵電大學 移動通信技術重點實驗室,重慶400065)

