摘 要: 將基于頻率響應屏蔽(FRM)方法的FIR濾波器設計與多速率數字信號處理應用到數字下變頻器" title="下變頻器">下變頻器設計中,同時利用CSD數對濾波器系數進行優化,大大降低了運算量和算法復雜度。
關鍵詞: 軟件無線電" title="軟件無線電">軟件無線電 數字下變頻器(DDC) 頻率響應屏蔽技術(FRM) 標準有符號數字量(CSD) 多速率信號處理
軟件無線電(Software Radio)的基本思想是把A/D、D/A變換器置于收/發信機的天線之后,用軟件實現無線電系統的所有功能[1]。軟件無線電技術實現的通信系統造價低廉,靈活性強,因此成為研究的熱點。由于軟件無線電系統強調盡量接近射頻端進行采樣,運算量很大,嚴重阻礙了它的應用,這就是所謂的DSP瓶頸。數字下變頻器(DDC)是其中運算復雜度最高的處理單元,因此,研究其低運算量結構在軟件無線電系統的設計具有重要意義。
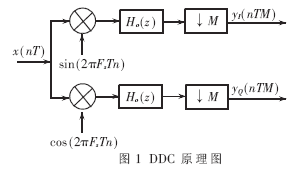
數字下變頻器結構如圖1所示。其運算復雜度主要由ADC采樣率和低通信道選擇濾波器的階數P決定。在軟件無線電系統中,ADC位于射頻或高中頻,因此Fs很高;同時,信道選擇濾波器的過渡帶寬很窄,因此階數P很大。本文將研究多速率信號處理技術與濾波器設計技術相結合的方法,通過把混頻和濾波操作放在降采樣之后,降低濾波器階數和改進乘法器結構提高DDC實現效率。首先引入一種特定的基于FRM方法的FIR濾波器實現結構;然后基于此類濾波器實現DDC,并使用CSD對乘法器系數進行優化,計算復雜度,討論相對傳統方法的優越性;最后,給出仿真結果。
1 基于FRM技術的FIR濾波器實現方法
基于FRM技術實現的FIR濾波器如圖2所示[2]。它包含兩個并聯的支路,每個支路由兩個級聯的FIR濾波器組成。
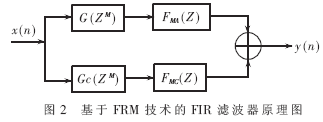
由此法合成的FIR濾波器過渡帶寬為G(Z)過渡帶寬的1/M,一般情況下比屏蔽濾波器的過渡帶寬要小得多。由于濾波器的階數P與過渡帶寬成反比,故當要求的FIR濾波器相對過渡帶寬很窄時,以FRM結構實現FIR濾波器比直接形式實現FIR濾波器具有更低的計算復雜度。
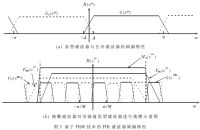
G(Z)和GC(Z)是兩個互補的FIR濾波器。它們的頻率響應滿足G(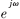 )+GC(
)+GC(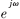 )=1,當濾波器傳遞函數(如圖3(a)所示)時,其沖激響應是奇對稱的,同時除了h(0)=
)=1,當濾波器傳遞函數(如圖3(a)所示)時,其沖激響應是奇對稱的,同時除了h(0)=
1/2外,僅在n=(2k-1)時,h(n)取非零的純虛值,因此計算復雜度較低。本文采用通帶截止頻率" title="截止頻率">截止頻率為π/2的升余弦滾降濾波器右移π/2獲得。
掩膜" title="掩膜">掩膜濾波器FMA(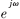 )和FMC(
)和FMC(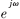 )使用通帶截止頻率為ωMP=((4I-1)·π)/(2M)的低通濾波器" title="低通濾波器">低通濾波器分別乘以exp(-j(π-2△)n/2M)和exp(j(π-2 △)n/2M)獲得,因此兩個掩膜濾波器的沖激響應互為共軛。
)使用通帶截止頻率為ωMP=((4I-1)·π)/(2M)的低通濾波器" title="低通濾波器">低通濾波器分別乘以exp(-j(π-2△)n/2M)和exp(j(π-2 △)n/2M)獲得,因此兩個掩膜濾波器的沖激響應互為共軛。
對兩個互補濾波器進行插值,即每個時延用M個時延代替,得到原型濾波器。假設G(Z)的過渡帶寬為2△,則原型濾波器的過渡帶寬為2 △/M。使用掩膜濾波器FMA(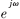 )和FMC(
)和FMC(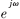 )對原型濾波器進行掩膜,獲得通帶截止頻率為(2Iπ- △)/M,過渡帶寬為2 △/M的低通濾波器。如圖3(b)。
)對原型濾波器進行掩膜,獲得通帶截止頻率為(2Iπ- △)/M,過渡帶寬為2 △/M的低通濾波器。如圖3(b)。
令fMA(n)=fRE(n)+j·fIM(n),則fMC(n)=
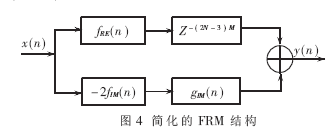
fRE(n)-j·fIM(n),其中FRE(n)和FIM(n)均為實序列。假設原型濾波器的沖激響應為g(n)=δ(n)/2+j·gIM(n)。濾波器總的沖激響應為[1]: h(n)=gM(n)·fMA(n)+gCM(n)·fMC(n)
=fRE(n)-2·fIM(n)·gIM(n)(2)
因此濾波器結構可簡化為如圖4,其中(2N-3)為原型濾波器的階數。
2 高效DDC實現結構
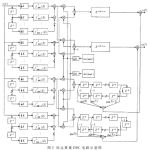
通過適當選擇參數,可以使得M整除K。利用多速率數字信號處理理論[3],采用濾波器系數多相分解的方法,可以將降采樣提前到混頻和濾波器之前。由于大量運算放在低采樣率一邊,因此大大降低了運算量。具體變換方法參考文獻[4],這里不再贅述。具體實現電路見圖5。
由于采用了多相濾波與混頻相結合的方法,必須對濾波器系數進行變換。其中各濾波器的系數變換為:
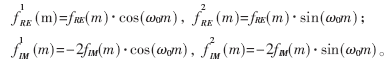
3 CSD碼優化濾波器系數
CSD碼優化濾波器系數是一種比較好的減少運算量的辦法[5],如圖6所示。一個整數X與另一整數Y的乘積的二進制表示可以寫成:
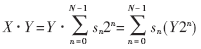
對于標準二進制,由于sn=0時對應項Y2n并不參與累加運算,可以用另一種表示方法使非零元素量降低,使加法器的數目減少,降低硬件的規模和運算量。有符號數字量(SD)有三重值{0,-1,+1},如果任意兩個非零位均不相鄰,即為標準有符號數字量(CSD)。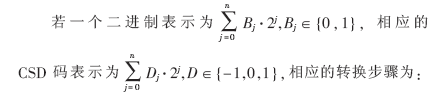
① 從B的最低位,設標志j=0,置初始進位C0=0;
② 用Bj+1,Bj和進位Cj以傳統二進制算法生成進位Cj+1;
③ 生成D的第j個數Dj=Bj+Cj-2Cj+1;
④ j+1,并重復步驟②直到j=n。
可以證明CSD表示對給定數是惟一的并且是最少非零位的。研究表明,變換M位字長的二進制補碼數為CSD碼,非零位的數目可減少到平均數的1/3。其流程圖如圖7所示。
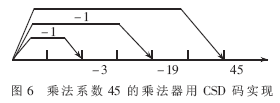
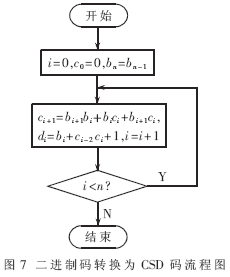
由于本文設計的DDC中使用的乘法除了幾個混頻操作外都是固定系數的,因此可用CSD碼優化濾波器系數以減少系統所需的資源。
4 DDC的仿真實現和計算復雜度分析
本文使用simulink算法設計了一個數字下變頻器進行計算機仿真驗證。具體指標如下:
ADC采樣率為140MHz,載波頻率為35MHz,降采樣系數K為4,M為20。在140MHz的采樣率下設計掩膜濾波器原型濾波器,其中掩膜濾波器由通帶截止頻率位12.25MHz,過渡帶寬為3.5MHz,阻帶衰減為20dB的59階低通濾波器乘以exp(-jnπ/40)獲得。原型濾波器由截止頻率為35.0MHz(-6dB),滾降系數0.01的升余弦滾降濾波器乘以exp(-jnπ/2),并將濾波器中的Z-1替換為Z-20獲得。設計出來的低通濾波器通帶截止頻率為14MHz,過渡帶寬為0.2MHz,阻帶衰減為20dB。
仿真得到的DDC頻幅特性如圖8(a)。低通濾波器的過渡帶非常窄,14.2MHz的信號比14.0MHz大約衰減了20dB。圖8(b)和(c)分別是相同幅度的14.0MHz和14.2MHz信號調制在35MHz載波上后,經DDC處理的頻譜輸出。圖8(d)、(e)、(f)是將14.2MHz和14.0MHz相加、用35MHz載波調制、經DDC處理輸出的頻譜輸出。可見(d)中輸入頻譜在14.2MHz的能量峰在輸出頻譜(f)中被濾除了。
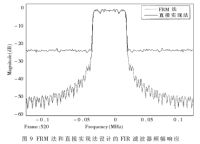
本文利用simulink自帶的濾波器設計軟件,以直接實現的方法設計了一個600階的通帶截止頻率為14MHz,過渡帶寬為0.2MHz,阻帶衰減為20dB的FIR濾波器,并與利用FRM技術設計的160階FIR濾波器進行比較。如圖9所示,在通帶部分,兩個濾波器有著幾乎完全相同的頻幅響應;FRM法比直接實現法獲得了更好的阻帶衰減,改進了濾波器的性能。在耗費的資源方面,由于多相分解與混頻相結合的緣故,掩膜濾波器有一半的系數為零,因此只用了100個固定系數乘法;由于濾波和混頻都在降采樣之后,因此每個乘法器單位時間的運算量為原來的1/4;再估算由于采用了CSD數對濾波器系數進行了優化,所需乘法器資源是未優化時的1/3。綜上所述,實現本系統所需要的硬件資源僅為常規方法實現的數字下變頻的(100/500)×1/4×1/3=1/60,大大緩解了DSP瓶頸。
本文針對軟件無線電中的寬帶信號處理,參考多速率信號處理和FRM以及CSD等優化技術,設計出一種FIR信道選擇濾波器并將其應用于DDC之中。這種濾波器在改進了性能的同時大大降低了運算量,極大地緩解了軟件無線電系統的DSP瓶頸。
參考文獻
1 Zoran Salcic, Christoph F. Mecklenbrauker, software radio-architectural requirements, research and development chal-lenges, ICCS 2002,2002;(2):711~716
2 ZHANG Y L, WU W L, TIAN B Y. A novel sharp-cutoff FIR filter design technique and its application in software radio. Proceedings of ICCT2003, 2003;(2):1821~1825
3 胡廣書.數字信號處理-理論、算法與實現.北京:清華大學出版社,1997:281~296
4 高志成,肖先賜.寬帶數字下變頻的一種高效實現結構.電子與信息學報,2001;23(3):255~260
5 Hasan Y M, Falkinburg M, Helwig A. Canonic signed digit FIR filter design. Signals: Systems and computers,2000;(2):1653~1656