??? 摘?要： 基于軟判決譯碼規則，采用完全并行的解碼結構，使用Verilog硬件描述語言，在Xilinx公司的FPGA（Virtex-2 xcv1000）上實現了碼率為1/2、幀長為20bit的規則（3,6）LDPC碼的譯碼器" title="譯碼器">譯碼器，最大" title="最大">最大傳輸速率" title="傳輸速率">傳輸速率可達20Mbps。對LDPC碼的實際應用具有重要的推動作用。
??? 關鍵詞： LDPC碼? 變量節點? 校驗檢點? 因子圖? 譯碼
?
??? 在通信系統中糾錯碼" title="糾錯碼">糾錯碼被用來提高信道傳輸的可靠性和功率利用率，低密度奇偶校驗碼(LDPC碼)是目前最逼近香農限的一類糾錯碼。1962年，Gallager[1]首次提出了LDPC碼的古典模型,即規則（regular）的LDPC碼：(n,j,k)，校驗矩陣H具有恒定的列重量和行重量。LDPC碼由于比Turbo碼更接近香農限的誤碼率性能[2]和完全并行的迭代譯碼算法使其比Turbo碼在部分場合具有更廣泛的應用前景，從而使LDPC碼成為當前糾錯編碼的一個研究熱點。基于良好的譯碼性能，LDPC碼被認為是通信系統的下一代糾錯碼。
1 規則LDPC碼
1.1 因子圖描述
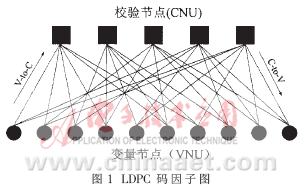
??? 因子圖[2]有兩類頂點，分別為變量節點(variable nodes,用空的圓點表示)和校驗節點(check nodes,用方框表示)。Tanner圖就是這兩類頂點之間的二部圖，即每條邊的一端與變量節點相連，另一端與校驗節點相連。變量節點代表實際的變量，校驗節點代表這些變量節點之間的約束。對于（j，k）-LDPC碼的每個變量（bit）都受j個校驗(check)的約束，因此每個變量節點應該連接j個校驗節點。每個校驗方程有k個變量，因此每個校驗節點應與k個變量節點相連。由于LDPC是一種線性碼，使得它的因子圖一邊為變量節點，一邊為校驗節點，故LDPC碼的因子圖表示有專用的定義：二部圖（bipartite graphs）。
??? 圖1表示了校驗矩陣為H的規則（3，6）LDPC碼的因子圖，它是由10個變量定點和5個校驗定點組成的二部圖，邊剛好對應于矩陣中1的位置，這種因子圖是LDPC迭代譯碼算法的基礎。
?
1.2 LDPC碼的譯碼算法
??? LDPC碼的譯碼采用信度傳播（belief-propagation或BP）算法[1]，它與因子圖相對應，如圖1所示，利用BP算法獲得好的譯碼性能，LDPC碼的因子圖中環的長度必須盡可能地長，長度為4的環會降低BP算法的性能，H矩陣設計時應避免出現。如果直接使用BP算法，由于在迭代過程中存在大量的乘運算，將使硬件的復雜度大幅度上升，本論文采用改進的Log-BP算法[1][4]，把大量的乘運算轉換成加運算，從而降低硬件復雜度及生產成本。
??? 首先定義可能用到的幾個變量及符號的意義：H表示一個M×N的LDPC校驗矩陣，Hi,j表示矩陣H中第i行第j列的元素。定義校驗節點m上的第n個變量節點為N（m）＝{n:Hm,n=1}，關聯在變量節點n上的第m個校驗節點為M(n)={m:Hmn=1}。定義校驗節點m上關聯的除了第n個變量節點以外的所有變量節點為N(M)n，變量節點n上關聯的除了第m個校驗節點外的所有校驗節點為M(n)m。
??? Log－BP算法的譯碼過程：
??? 輸入數據：初始概率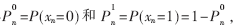
n=1, …, N;
??? 輸出數據" title="輸出數據">輸出數據：硬判決結果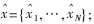
??? 譯碼過程：
??? 初始化：對于接收到的每個變量節點n計算初始信道信息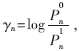
并對每個點計算初始信息，其中（m,n）∈{(i,j)|Hi j=1}。
??? 
??? 迭代譯碼：
??? (1)校驗節點計算
??? 
??? 
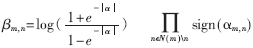
???? 對于每個變量節點n，在完成變量節點計算后，對
??? (3)判決條件
??? 
??? 
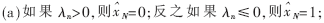
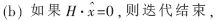否則跳到第2步迭代譯碼部分，直至校驗成功或者達到最大迭代次數。
??? 上面算法中的αm,n和βm,n都被稱為外部信息，其中αm,n是從變量節點向校驗節點傳遞的信息，βm,n是從變量節點向校驗節點傳遞的信息。通過log－BP算法和BP算法的比較可以發現，log－BP算法中除了f(x)=log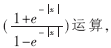
剩下的都是加法運算，從而避免了BP算法中乘運算過多的弊病。在本文中函數f(x)利用FPGA中的查找表（Look-up Table, LUT）實現。
2 H矩陣的生成
??? Gallager提出的LDPC碼的H矩陣[1]必須滿足以下兩點：
??? (1)H矩陣的每一列有j個1，j>=3;
??? (2)H矩陣的每一行有k個1，k>j;
??? 本文中選擇j=3,k=6,通過編程用matalab軟件生成若干滿足條件的H矩陣，選擇其中一個性能最好的H矩陣進行LDPC碼的fpga譯碼實現。當n=20時，最終選擇H矩陣如圖2所示。
?
?
3 LDPC碼完全平行譯碼結構
??? 由二部圖可以直觀地看出，變量節點計算需要的信息只需由校驗節點來提供，校驗節點計算需要的信息只需要由變量節點來提供，譯碼器在設計時可以給每個變量節點分配一個變量節點處理單元（Variable Node processing Unit，VNU），給每個校驗節點分配一個校驗節點處理單元（Check Node processing Unit，CNU），從而實現譯碼器的完全并行結構。
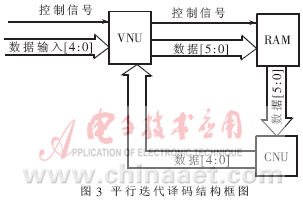
??? 譯碼器的核心模塊是迭代譯碼部分，迭代譯碼的結構與算法是緊密相連的，譯碼結構的確定必須在仔細分析算法的基礎上，迭代譯碼的過程是CNU和VNU模塊計算結果的相互傳遞和更新。如果直接將CNU和VNU連接，不但不容易控制迭代的過程并且可能出現不穩定狀態，所以需要在CNU和VNU之間安插RAM以起到數據的緩沖和控制作用。輸入、輸出模塊分別控制數據的輸入和輸出，當條件滿足或者是迭代完成時，讀入數據并把迭代結果輸出。
3.1 迭代譯碼結構
??? 圖3表示平行迭代譯碼結構[5][6]。其中只畫出兩個節點之間一條數據通路的連接方式，因為是完全平行迭代譯碼結構，其他節點之間數據通路的連接方式與此相同。信道初始化數據送入VNU模塊進行數據處理后，送入RAM模塊，數據經過CNU模塊，最后再送入VNU模塊，這樣就完成一次迭代。數據信息從VNU到CNU與數據信息從CNU到VNU分別在不同的數據線上傳輸（圖1）。
?
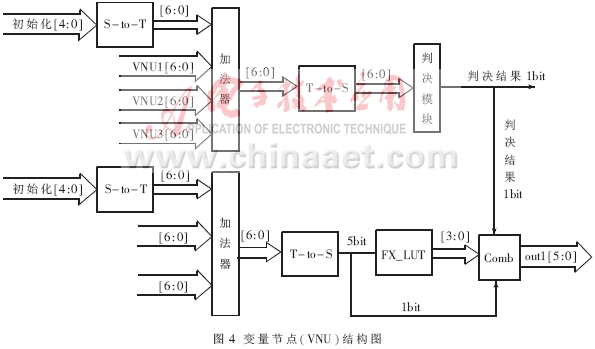
3.2 變量節點結構（VNU）
??? 變量節點的結構如圖4所示。從中可以看出每個變量節點的度為3（j=3），四個5 bit輸入信息包含一個信道信息和三個與之相連的校驗節點的信息。由log-BP算法可以看到α進行的是量化值的計算，沒有牽扯到符號位，而γm,n和λn的計算都有包含符號位的相加，實際上其中還包含了減法運算，而本文采用的符號信息位的格式不能用于減法運算，需要將其轉換為其他格式。在本文進行和運算時，首先將其轉換為二進制補碼形式，運算結束后再轉換回符號量化位格式，查表(FX_LUT)進行f(x)運算。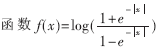
可由FPGA中的邏輯單元LUT來實現。Comb模塊把1bit的判決結果x、4bit的查找表運算結果與符號位合在一起作為外部信息送入校驗節點(CNU)。圖4上半部分為輸出譯碼的結果，下半部分為三個數據輸出通道中的一個，其余兩個的結構與此完全相同，唯一不同的是加法器的輸入， 根據log-BP算法，其中初始化數據經過S-to-T轉換后的數據輸入固定，另外兩個輸入數據為其他兩個數據通道的輸入經過S-to-T轉換后的數據。
?
?
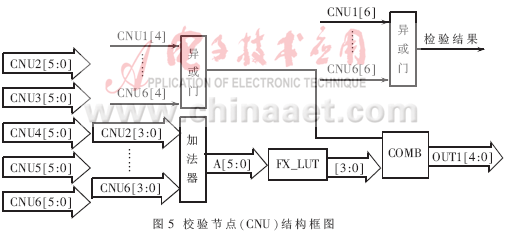
3.3 校驗節點結構（CNU）
??? 校驗節點(CNU)結構如圖5所示，每個檢驗節點的度數為6(k=6)，圖5只畫出數據的一個輸出通道，其余5個輸出通道的結構與此完全相同，加法器為檢驗節點首先對外部信息中的判決結果進行驗證，看是否滿足H·xT=0，滿足則結束迭代。CNU模塊中f(x)的x計算是只計算量化值而不管正負的，而本譯碼器采用的符號量化位格式只需將符號位屏蔽即可得到相當于絕對值效果的量化位運算，也就是CNU模塊中不需要將符號量化位轉化為二進制補碼形式。
?
3.4? 數據輸入與輸出
??? 完全平行譯碼結構可以分為三部分：迭代譯碼模塊、數據輸入模塊和數據輸出模塊。因為是完全平行譯碼方式，輸入數據經過串并轉換后，同時讀入VNU進行迭代計算。在數據輸出模塊，每一次迭代完成要進行條件判別，如果CNU所有的校驗結果都為零，則輸出數據。或者已經完成17次迭代，此時強制輸出數據。數據的輸入與輸出分別用不同的時鐘進行控制。圖6為譯碼器其中一幀數據的測試結果，編碼之前的信息為01010101，圖6中OutData為編碼后數據的輸出。
?
4? FPGA實現
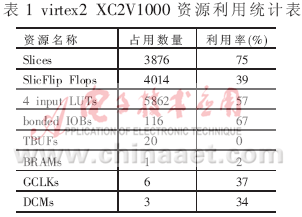
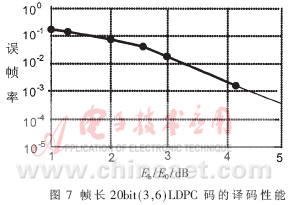
??? 根據規則（3，6）LDPC碼的完全平行譯碼結構，選擇在Xilinx Virtex2 XC2V1000-fg256上對其進行物理實現，譯碼器采用Verilog硬件描述語言編寫，用Xilinx的開發工具ISE6.1在XC2V1000上對譯碼器進行布局布線。硬件資源的占有率如表1所示。通過時序分析可以看出，譯碼器的最大時鐘頻率為20MHz,以輸入時鐘為基準，完成17次迭代最多需要20個時鐘，完成一幀數據的輸入需要20個時鐘，可以得出譯碼器的最大譯碼速率為：V=20×20/20=20Mbps。圖7為幀長為20bit的LDPC碼的譯碼性能，因為碼長較短，性能沒有達到最好。這為更高速 LDPC碼譯碼器的設計打下堅實的基礎，碼長為1024bit，傳輸速率可進一步提高，甚至達到1Gbps,譯碼性能會更好[6][7]。
?
?
??? 本文基于軟判決譯碼規則，采用完全平行譯碼結構，設計出幀長為20bit，碼率為1/2的規則（3，6）LDPC碼的譯碼器，在Xilinx virtex2 XC2V1000-fg256上對其進行物理實現，最大迭代次數為17次，傳輸速率達到20Mbps。LDPC碼具有良好譯碼性能，與Turbo碼相比更易于硬件實現，并能得到更高的譯碼速度。下一步將設計出碼長為1024bit或碼長更長的LDPC譯碼器，進一步提高傳輸速率，降低誤碼率，為加速該技術在中國的商用奠定基礎。
參考文獻
1 R.G. Gallager.Low density parity check codes.IRE Trans. Inform. Theory,1962； IT-8（Jan）：21～28
2 R. M. Tanner. A recursive approach to low complexity?codes.IEEE Trans. Inform. Theory，1981; IT-42:533～547
3 M. Chiani, A. Conti, and A. Ventura.Evaluation of lowdensity parity-check codes over block fading channels. in??2000 IEEE International Conference on Communications.?2000：1183～1187
4 S. Kim, G. E. Sobelman, J. Moon.Parallel VLSI Architectures for a Class of LDPC Codes. Circuits and Systems.IEEE International Symposium on, 2002;Volume:2
5 C. J. Howland and A. J. Blanksby.Parallel decoding architectures for lowdensity parity check codes. in Proc. IEEE?ISCAS,2001;4(5):742～745
6 A. J. Blanksby and C. J. Howland. A 690-mW 1-Gb/s?1024-b, rate-1/2 low-density parity-check code decoder.?IEEE Journal of Solid-State Circuits,2002;37(3)：404～412
7 T. Zhang and K.K. Parhi.VLSI implementation-oriented（3,k）egular low-density parity-check codes. IEEE Workshop on Signal Processing Systems (SiPS), 2001;9