配漿濃度是決定造紙生產工藝質量的重要指標。近年來，隨著制漿造紙技術的飛速發展，業內對配漿濃度控制的精度提出了越來越高的要求。然而由于配漿濃度控制過程中，工藝參數常常發生較大變化，系統模型難以建立，傳統控制器不能始終保持最優運行，有時甚至出現穩定性問題，導致現有配漿濃度控制手段存在一定的盲目性。因此提高配漿濃度的精度對節約成本、提高生產質量具有十分重要的意義[1]。

1 工藝描述
    造紙行業配漿系統主要完成配漿濃度、流量大小的測量與控制。草漿、木漿、損配漿按照一定的配比進入混合管然后送往紙機，另外在混合池里還要按比例加入一些化學添加劑和染料。該流程中各種漿料分別通過各自的濃度控制回路對其漿濃度進行獨立調節控制,因此濃度控制回路效果直接決定了最終的配漿結果[2]。
    濃度控制回路工藝如圖1所示，濃度控制由調節稀釋水量大小實現，流量大小由手動閥門粗調。配漿濃度測量采用刀式傳感器，流量測量采用電磁流量計，濃度控制執行器采用電動調節閥，濃度現場控制器是以單片機為核心、配以EPROM及實時時鐘構成的微控制器。對于間斷配漿過程，當設置一次配漿絕干量后，配漿單元自動啟動抽漿泵工作，從漿池中抽取混合料，同時開啟稀釋水閥門，調節配漿濃度。由于從漿池中抽取混合料的速度基本穩定，因而稀釋水流量直接決定了最終的配漿濃度，混合料與稀釋水混合后，累計以配漿絕干量計算，當累計配漿絕干量與設置的一次配漿總量相等時，自動停止抽漿泵工作。

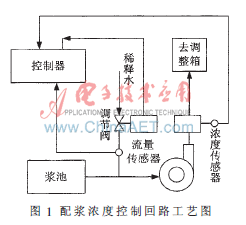
    為了保證配漿生產過程中，混合料濃度精度達到工藝要求，同時混合料濃度具有一定的抗干擾能力，其控制系統必須滿足以下要求:通過調節稀釋水閥門的開度，保證配漿濃度的控制精度在±0.08%內。
2  控制系統分析及結構
    由于配漿濃度控制系統具有較強的非線性和時變性，且造紙生產過程參數在生產過程中常常受到溫度、濕度的影響，很難構造出一個精確的數學模型，因此，采用常規控制往往出現頻繁波動，難以跟蹤給定混合料濃度，無法取得較好的運行效果。通過對配漿工藝研究分析，本文提出一種基于智能控制的雙閉環濃度控制方法，其控制原理如圖2所示。該系統是由模糊遺傳算法、神經網絡PID、控制閥組及傳感器組成的一種直接數字反饋串級控制系統。

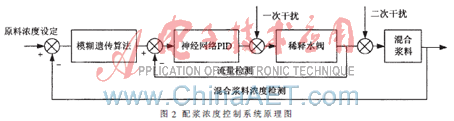
    該控制系統由內外兩個閉環控制構成，外環為濃度控制環，內環為流量控制環。首先，濃度控制系統利用混合料濃度設定值和混合料濃度檢測值計算得到系統濃度偏差，以其作為濃度控制環路的輸入，通過模糊遺傳控制器計算得到最優濃度調節量；然后，將該濃度調節量通過查表方式轉換為相應的稀釋水流量增量，作為流量控制環的輸入，內環通過調節稀釋水流量達到調節混合料濃度的目的，利用神經網絡PID模塊對稀釋水濃度進行調節，始終保證混合漿料濃度滿足工藝要求。
3 基于模糊遺傳算法的外環控制器設計
    在配漿濃度控制系統中，由于受到添加原料、開關漿池閘門等突發因素的影響，采用傳統的控制方法往往難以得到良好的作用，很難同時兼顧穩定控制、提高精度、抑制超調的要求。而且配漿濃度控制系統中，濃度傳感器檢測值會隨著具體環境、季節、晝夜變化產生漂移，而傳統模糊系統的隸屬函數等參數很難自動調整，難以適應這些變化。因此本文采用模糊控制器對配漿濃度變化進行模糊推理，同時采用遺傳算法對模糊控制器的參數進行自適應調整，從而得到最優的稀釋水流量。
3.1 模糊控制器的設計
    根據實際生產工藝的需要，模糊控制器根據當前混合料濃度的檢測值和設定值之間的偏差及其偏差變化率、模糊規則經推理得到最優的稀釋水流量設定值。混合料濃度模糊控制模塊的輸入變量為混合料濃度與設定值的偏差e及其變化率ec，輸出變量為稀釋水流量的增量Δu。
　　本控制器中，濃度偏差e [-10%, +10%]，論域E＝{-7,-6,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,6,7}，模糊變量的詞集選擇為{NL，NM，NS，O，PS，PM，PL}。濃度偏差變化率 ec∈[-0.4%/s,0.4%/s]，論域為EC ={-4,-3,-2,-1,0,1,2,3,4}，EC的模糊變量為{NL，NS，O,PS，PL}。
    類似地,稀釋水流量增量輸出Δu∈[-2m3/s,2m3/s]，論域U＝{-6，-5,-4,-3,-2,-1,0,1,2,3,4,5，6}，U的模糊變量為：{NL，NM，NS，O，PS，PM，PL}。
    根據現場調節的經驗發現,濃度偏差變化率ec僅在較大時方能反映出混合料濃度的變化趨勢。因此，控制增量U與偏差E的關系較為緊密，而EC則主要作為U的一個輔助參考變量。本模糊控制器把實際的控制策略歸納為如表1所示的控制規則表。

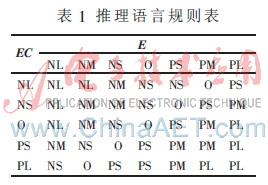
    為了抑制傳感器檢測中可能出現的異常值，本文對于輸入輸出變量、隸屬度函數均采用如下的梯形函數。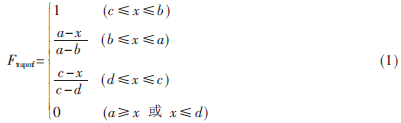

    由上述所設計的模糊推理規則及隸屬度，采用Mamdani模糊推理的重心法進行解模糊，得到模糊控制的查詢表如表2所示。系統將濃度偏差e及其變化率ec模糊化后求得E、EC，通過查詢表，得到控制輸出U，并將此值經過清晰化接口，求得稀釋水流量的增量Δu。

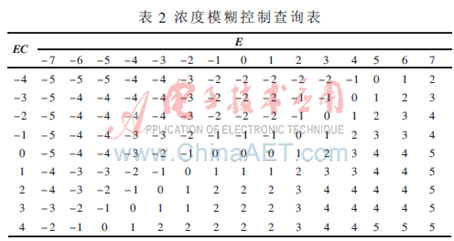
3.2 基于遺傳算法的隸屬度選擇
    遺傳算法(GA)具有搜索快速、易實現和計算效率高的優點[3]，非常適合在配漿濃度控制系統中。
3.2.1算法思路及步驟
　 本文在模糊算法的設計中采用了梯形隸屬度函數，其形式由4個參數確定，由模糊算法的3個輸入變量各自的梯形隸屬度函數參數，共同構成了遺傳算法的解空間。根據檢測環境選擇適應度函數，通過個體的變異搜索，尋找使得適應度函數最優的隸屬度函數解，即得到最優的模糊算法結構。利用遺傳算法選取隸屬度，其實現步驟為：
　(1)首輪隨機產生n個模糊隸屬度參數個體，組成初始種群，非首輪隨機產生n-1個個體，第n個個體為以前一代種群的最優個體，組成新一輪迭代的起始種群。
    (2)利用適應度函數評估個體適應度，以尋求在最合適各類傳感器運行狀態和配漿生產環境的模糊隸屬度函數解作為最優個體，并將其標識為種群中的第n個個體，然后將該個體保留為下一代種群成員。
    (3)選擇種群中所有個體(包括第n個個體)進行交叉操作。
　 (4)檢查當前種群是否符合名義收斂條件，如果滿足條件，則執行下一步，否則轉向(1)。
　 (5)如果滿足給定的優化條件，則終止優化過程，否則轉向(1)。
3.2.2隸屬度函數種群的編碼表示
    本文選用如式(1)所示的梯形隸屬度函數其描述，式中a、b、c、d是需要優化的參數。其中，b=c為三角形隸屬函數，b=a為降半梯形函數，c=d為升半梯形函數，但是b=a和c=d不能同時發生。根據這些參數的不同，可以影響梯形函數的形狀，產生不同的模糊集，從而對模糊推理的結果產生影響，使濃度控制算法具有較強的適應能力。隸屬度函數的參數種群，采用實數編碼方式,實數編碼染色體表度比二進制編碼的染色體長度短，編碼方式簡潔自然，減輕了遺傳算法的計算負擔，提高了運算效率，能夠更好地保持種群的多樣性。待編碼的參數為a、b、c、d,每條染色體有4×n×m。其中n為輸入變量的維數，m為混合料濃度模糊控制器中隸屬度函數的個數(本文取3)。對于第一條染色體其編碼如下：

3.2.3 適應度函數
    在算法進化中，個體適應度不僅需要考慮配漿濃度控制系統濃度跟隨設定值的準確性，還需要考慮模糊推理系統本身的合理性和解釋性。因此算法的適應度由兩個部分組成，一是配漿濃度控制準確性指標，二是模糊隸屬度函數的解釋性指標。
    配漿濃度控制準確性指標即為模糊控制器輸出的稀釋水流量應使得濃度與濃度設定值間的偏差最小。因此，采用如式(5)所示的性能指標。

式中，Js(u)表示以模糊控制器輸出的稀釋水流量計算出的混合料濃度，J為濃度設定值。
    模糊隸屬度函數的解釋性指標：首先,考慮模糊隸屬度隸屬函數劃分必須具有完備性，即保證隸屬度函數能全部覆蓋輸入和輸出變量的取值域，同時對于任何的輸入變量，在其論域內的任何值，至少有一個隸屬函數相對應，在形式上表現為隸屬函數之間存在位置的交叉；其次,隸屬函數劃分必須是可區分的，即對于同一變量，隸屬函數之間存在明顯的位置區別，以便賦予一定的語義項。如果在尋優過程中，出現相鄰的模糊集合的隸屬度函數之間無重疊，就不能保證對于取值域內的任意輸入都能找到一個模糊集合，即造成了隸屬度函數的不完備性。另外還可能出現一個隸屬度函數完全覆蓋另外一個函數，這種情況的出現也會導致模糊推理系統本身不合理，并且不具有解釋性。為了解決這些問題，相鄰模糊集合的隸屬度函數必須有一定的交叉率?琢。因此，模糊隸屬度函數的解釋性指標可表示為：

式(5)、式(6)的指標越小越好，采用分量加權求和，適應度函數為：

式中，加權因子v1、v2為正實數，預先根據經驗設定，本文取v1=0.4，v2=0.6。
3.2.4 變異策略
    目前使用較多的變異策略有點式交叉變異和均勻交叉變異。點式交叉破壞模式的概率較小，但搜索到的模式較少；均勻交叉破壞模式的概率較大，但搜索到的模式較多。本文中解空間達到了4×n×m個維度，相對較大，采用點式交叉會使算法的收斂速度較快，因此本文采用點式交叉策略。
3.2.5 雜交策略
    目前使用較為廣泛的雜交操作是單點雜交、兩點雜交和多點雜交。采用單點雜交、兩點雜交基因的變化較為緩慢，從而導致隸屬度函數選擇的周期增加，嚴重影響系統的整體效率，增加了配漿控制系統的滯后性。因此本文采用多點雜交的方式。
4 基于BP神經網絡PID的內環控制器設計
    配漿濃度控制系統中，稀釋水流量是調節配漿濃度的決定因素，但是稀釋水閥門的開度-流量特性易受到水壓、水量的干擾而常常發生變化。傳統的PID控制方法，很難適應閥門的非線性特性，導致實際造紙流程中稀釋水流量出現較大波動，精確度不高。神經網絡具有任意非線性逼近能力、自學習能力以及概括推廣能力，使系統具有自適應性[4-5]，可自動調節控制參數，提高控制性能和可靠性。因此本文將BP神經網絡與PID控制方法相結合，用于控制算法來稀釋水流量的調節。
4.1 算法結構
    本文所設計的基于神經網絡PID的稀釋水流量控制的結構如圖3所示。控制器由兩部分組成:傳統的PID控制器和BP神經網絡學習算法[6]。經典增量式PID的控制算法為：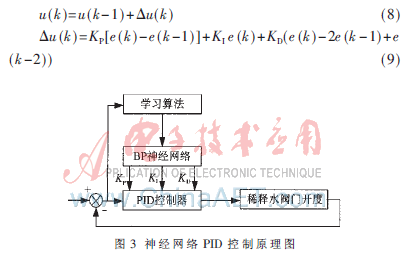

    神經網絡根據配漿控制系統的運行情況，通過網絡的自學習、權系數調整，使輸出層神經元對應PID控制器的3個可調整參數比例(KP)、積分(KI)、微分(KD)，以使得配漿濃度控制系統能適應閥門的開度-流量特性，使稀釋水流量跟隨模糊控制器的輸出值。
4.2 算法實現
    神經網絡隱層層數是神經網絡結構的重要參數，考慮系統本身復雜度、算法代價以及從實際應用效果，增加隱層后，稀釋水流量控制精度提高并不明顯。因此，本文采用一個隱層，與輸入層和輸出層共同構成三層BP神經網絡，其結構如圖4所示。

    按照梯度下降法修正網絡的權系數，即按E(k)對加權系數的負梯度方向搜索調整，并附加一個使搜索快速收斂全局極小的慣性項，由此帶來計算不精確的影響可以通過調整梯度下降法中的學習速度來補償。由以上分析可得網絡輸出層權的學習算法為：

5 應用及結論
    將本文所提出的配漿控制方法應用于岳陽某造紙廠,該紙廠原采用PID控制實際數據曲線如圖5所示，采用本方法控制系統實際數據曲線如圖6所示。控制系統中濃度設定值為17.55%，經過分析比較，該廠原有控制算法控制偏差超過0.12%的時間占采樣數據的60%，系統最大偏差為0.22%。而采用本文提出的控制算法，偏差超過0.07%的時間占采樣數據的10%，其余數據均穩定在0.07%范圍內，系統最大偏差為0.1%。從圖中可以看出，本文算法利用模糊控制的優點來彌補配漿濃度控制中的突發干擾和利用遺傳算法改善參數變化問題，同時利用神經網絡PID算法自學習特點，自動調節控制參數，以適應配漿生產過程中的開度-流量非線性，使得濃度的控制精度得到了較大提高，完全能滿足配漿過程濃度的工藝要求。

參考文獻
[1] 于秀燕．自動配漿控制系統[J]．黑龍江造紙，2004(1):50-52.
[2] LIAN R J, LIN B F, HUANG J H. A grey prediction  fuzzy controller for constant cutting force in turning [J].
International Journal of Machine Tool and Manufacture, 2005, 45(9):1047-1056.
[3] 馬清亮, 胡昌華, 楊青. 一種用于多目標優化的混合遺傳算法[J]. 系統仿真學報, 2004,16(5):1038-1040.
[4] CHOY M C, SRINIVASAN D, CHEU R L. Neural network for continuous online learning and control [J]. IEEE Transaction on Neural Network, 2004,17(4):1511-1531.
[5] SBARBARO D, JOHANSEN T A. Analysis of artificial  neural network for pattern-based adaptive control[J]. IEEE  Transaction on Neural Network, 2006,17(5):1184-1193.
[6] 劉紅波, 李少遠, 柴天佑. 一種基于模糊切換的模糊負 荷控制器及其應用. 控制與決策[J]. 2003, 18(5): 615-
618.