無線通信用戶數目日益增多,人們對業務種類及服務質量的要求越來越高,從以前的保證通話發展到今天的大容量、高速率通信,使得通信頻段變得日益擁擠,提高頻帶的利用率,解決頻譜資源緊張成為日益尖銳的問題。目前,廣泛采用的有碼分多址(CDMA)、線性調制,正交頻分多址(OFDM)等技術來解決此問題,但這些技術對功率放大器(PA)有嚴格的線性度要求,否則系統性能就會嚴重惡化。
預失真的基本思想是在放大器前構造放大器的逆特性,使得預失真器和放大器的聯合特性呈線性。本文是在這種思想的指導下,對預失真器的自適應算法進行改進,采用最小均方誤差(LMSE)方法,在μ的選擇上,使用分段變步長法,在均方誤差降低到25%范圍內使用大步長μ1,在剩余的25%范圍內使用小步長μ2,從而提高收斂速度,兼顧穩定性,完善預失真算法。
1 自適應濾波器
所謂自適應濾波器,是指根據濾波器的輸入輸出之間的關系,利用自適應算法來調節濾波器的系數,使得理想輸出與實際輸出之間的差值最小。
1.1 自適應濾波器的介紹
自適應濾波器它包括兩部分,一部分是數字濾波器,一部分是自適應算法,可用于自適應濾波器的通常有兩種,一種是無限長單位沖激響應數字濾波器(IIR),另一種是有限長單位沖激響應數字濾波器(FIR),一般采用FIR濾波器作為自適應濾波器的首選,FIR濾波器的方框圖如圖1所示。
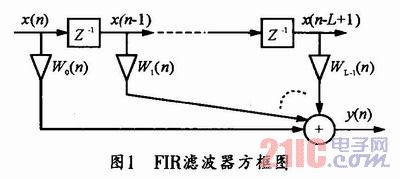
輸入與輸出之間的關系可表達如下:

1.2 傳統自適應算法
在自適應算法中,通常采用均方誤差(MSE)來衡量性能指標是否達到最佳狀態
![]()
當ε(n)取最小時,此刻所對應的一組加權系數W0(n為最佳系數。
最陡下降法是一種遞推方法,它系數迭代方程如下
![]()
其中μ為收斂因子,它控制著濾波器的穩定性及收斂速度,當μ越大,收斂速度越快,反之,收斂速度越慢,▽ε(n)表示誤差函數相對于w(n)的梯度,對加權向量的連續修正,將最終導致最小均方誤差εmin,此時加權向量達到最佳值w0。
LMS算法采用了瞬時平方誤差e2(n),用以估計MSE,克服了d(n)與x(n)統計特性未知的問題,即

1.3 改進的自適應算法
上一節介紹了傳統自適應算法,鑒定一個算法的好壞有幾個性能指標,分別是穩定性及收斂速度。
LMS算法要保證穩定性,μ必須滿足:

其中λmax是輸入相關矩陣R的最大特征值。而當濾波器的階數L很大時,λmax的計算量也很大,利用(11)式對μ的約束比較困難,在實際應用中有一種簡單的設計方法,設定

其中Px表示輸入信號x(n)的功率,利用(12)對μ的約束選取μ時,計算量明顯減小每一種自適應模式都有其自身的時間常數,MSE的時間常數可定義為

當μ較小時,τmse越大,收斂速度越慢,反之,收斂速度越快。
介于在μ的選擇上存在的一些矛盾,而在傳統自適應算法中μ為固定值,無論在穩定性及收斂速度方面都無法完全滿足系統的需求,本文采用了一種折中的方法,在信號處理初期,即25%emax
2 功率放大器及其預失真模型
當信號帶寬遠小于PA固有帶寬時,記憶效應可忽略,但當傳輸寬帶信號時,PA的記憶效應變得明顯,若仍采用無記憶的預失真技術,線性化效果將出現顯著惡化。
本采用間接的訓練結構來構造預失真器,它不需要知道放大器的具體模型和參數,因此被廣泛采用。模型原理圖如圖2所示。
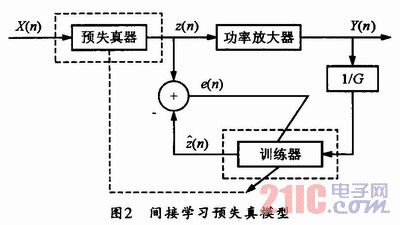
其中,x(n)為輸入信號,y(n)為的輸出信號,功率放大器的輸出信號經過乘法器1/G,G為理想功放增益,輸入預失真訓練器,通過預失真器得到輸出信號為,訓練器與預失真器的參數完全相同,理想情況下,
=z,e(n)=0,根據前幾節介紹的自適應算法,更新預失真器的參數,使得e(n)趨向于0,從而達到線性放大的目的。
間接學習模型中的功放是一個Wiener模型,為一個線性時不變系統(LTI)與一個無記憶非線性模塊(NL)的串聯;預失真器為與Wiener模型具有逆特性的hammerstein模型。
用a1表示線性Wiener模型中LTI的系數,bk表示NL的系數,功率放大器的代數表達式為

3 系統仿真
本論文中的算法,通過matlab仿真平臺進行仿真,來檢測算法對帶外失真的改善程度,并且檢測了算法的收斂速度,輸入信號為WCDMA信號,預失真器中無記憶非線性部分的最高階取K=5,線性時不變系統部分長度取Q=7,功率放大器模型具有與其相同的多項式階數和記憶深度。
3.1 系統仿真
從實際功放中得到系數a1=14.9740+0.0519j,a3=-23.0954+4.9680j,a5=21.3936+0.4305j,通過分段變步長得到線性時不變系統的系數bk及無記憶非線性系統的系數cl的估值分別為

經過仿真后得到頻譜圖如圖3所示。
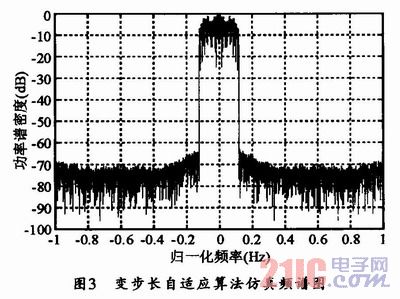
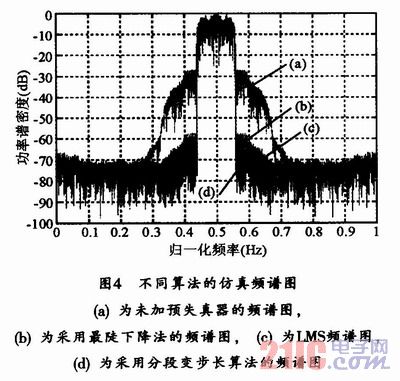
在同一系統中,采用同樣的方法針對最陡下降法和LMS算法進行仿真,并與分段變步長算法的仿真結果進行比較,得到頻譜圖如圖4所示。
3.2 性能比較
采用歸一化均方誤差(NMSE)來表征計算的收斂速度和計算精度,其表達式為
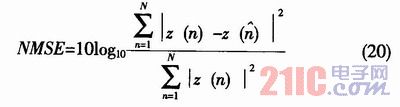
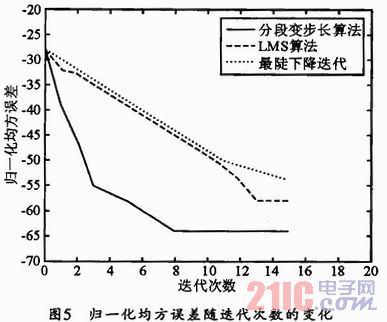
每迭代一次,按上式求出NMSE的值并記錄,三種自適應算法得到的仿真結果如圖5所示,分段變步長算法的迭代次數明顯少于最陡下降法及LMS算法。
采用誤差矢量幅度(EVM表征帶內失真,相鄰信道功率比ACPR表征帶外失真。
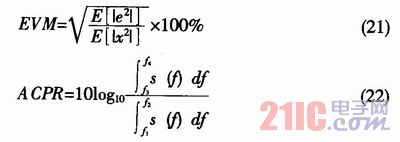
其中,s(f)為功率譜密度, [f1,f2]為傳輸信道,[f3,f4]為相鄰信道。
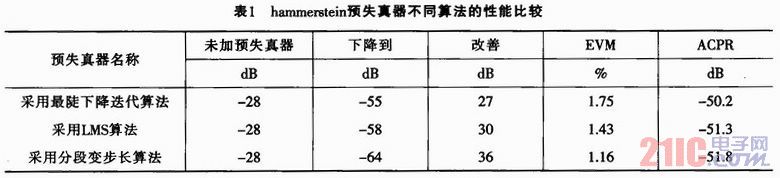
按照(21)與(22)兩式分別計算最陡下降法、LMS算法及分段變步長算法,得到結果如表1所列。
4 結束語
本文采用Wiener模型作為功率放大器,與之相逆的hammerstein模型作為預失真器,用間接學習的預失真方法,采用三種不同的自適應算法最陡下降法、LMS算法、分段變步長算法進行系統仿真比較,通過matlab仿真結果表明,分段變步長自適應算法不僅在收斂速度(迭代次數)上明顯優于其他兩種自適應算法,并在帶內失真與帶外失真較之其他兩種算法也有明顯改善。

