摘  要： 拓撲分析是電網分析的基礎。本文主要討論了電網拓撲分析算法及流程。在圖形建模的基礎上，提出了通過元件整合預處理過程減少參與拓撲計算的電氣元件的數量，從而提高計算速度的方法，最后介紹了算法的實現。
關鍵詞： 電網；拓撲分析；算法

　電力系統的網絡拓撲分析主要用來處理開關狀態的變化對電網結構產生的影響，是各種電網分析軟件的基礎。因此，電網拓撲分析的快速性和準確性就顯得尤為重要[1]。
　目前，網絡拓撲分析方法主要有樹搜索法和矩陣法兩種。樹搜索法分為深度優先搜索法和廣度優先搜索法，矩陣法分為鄰接矩陣法和關聯矩陣法。
1 不同拓撲分析算法的比較
　在參考文獻[1]中對不同拓撲分析算法進行了分析和比較，并得出以下結論：對環型電網，矩陣法比深度優先法有優勢；而對發散型電網，兩者則相差無幾。起始節點的選擇對矩陣法和深度優先法的拓撲速度影響很大，而對節點融合法和廣度優先法則影響不大。
　在拓撲分析算法的具體實現上，深度優先法原理簡單，編程易于實現，但運行時占用系統資源較多；而廣度優先法則能夠節省系統資源，但原理復雜，對編程技巧要求較高。
2 提高拓撲分析速度的方法
　在實際應用中發現，不論采用那一種拓撲算法，隨著電網規模的擴大，網絡的節點數和支路數的增減，拓撲計算量都會迅速增加，從而降低拓撲計算的速度。因此減少參與拓撲計算的電力元件數量，將有效提高拓撲計算的速度。
　考慮到只有開關狀態的變化才會改變電網設備的帶電狀態，在拓撲分析計算之前，對電網模型進行元件整合后，再進行具體的拓撲分析計算，具體的處理流程如圖1所示。

2.1 電網建模
　本文采用方便實用的圖形建模系統[2]。系統將表示實際設備的圖形元件定義為圖形和端口的集合，以不同圖形表示元件的不同類型，以端口來建立元件之間的連接。每個電力元件都擁有單個或多個端口，當不同元件的兩個端口重合時，即表示兩者連接。在繪制接線圖時就自動生成相應的拓撲關系，并作為連接屬性存放在元件中。另外，每個元件均設置如下屬性，以便在元件整合和后續的拓撲分析計算時使用：
　State：帶電狀態，0為不帶電（缺省），1為帶電；
　SearchNo：遍歷途徑的序號，0為尚未遍歷（缺省）；
　NetNo：所在子網號，0為尚未分配子網號（缺省）。
2.2 元件整合
　元件整合的目的是減少參與拓撲計算的電力元件的數量。其基本原理是以開關等能夠改變電力元件帶電狀態的設備為分界點，將其他電力元件整合為一個虛擬的電力元件。該虛擬元件具有與實際的電力元件相同的屬性，并擁有一個或多個端點，用于與開關元件的連接。具體整合過程如圖2所示。當對電網模型中的元件進行遍歷時，如果該元件是開關，則不做任何處理；否則，如果已存在的虛擬元件中不包括該元件，則創建新虛擬元件；同時如果該元件與開關連接，則創建虛擬元件與開關的連接關系，否則將這兩個元件整合到一個虛擬元件。

2.3 拓撲計算
　本文參與拓撲計算的是通過整合后的只有虛擬元件和開關的電網模型，而計算的主要任務是處理由于開關變化所引起的電網元件帶電狀態的變化，因此對參考文獻[3]的算法流程進行了優化。具體計算流程如圖4所示。

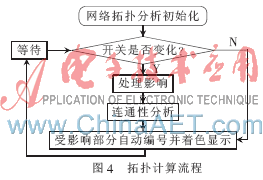
　其中網絡拓撲初始分析包括初始廠站分析、自動節點編號（形成節點-支路關聯表）、初始連通性分析（得到電氣島號）。當開關狀態發生變化的時候，根據支路-節點關聯表，進行連通性分析，相當于電氣島分析。分析的結果按照帶電與否在電力元件上進行著色，顯示在電網接線圖上，使拓撲的結果一目了然。
3 算法實現

　本算法采用C++語言，在Window操作系統平臺上得到了實現。算法軟件由4個模塊組成，各模塊的具體功能如下。
　圖形建模模塊：用于繪制電網接線圖，同時完成電網建模的功能。接線圖以文件的形式存儲在計算機中，電網模型存儲在商用數據庫中。
元件整合模塊：分析圖形建模模塊生成的電網模型，并將其轉換為由虛擬元件和開關元件組成的新的電網模型，新的電網模型存儲在商用數據庫中。該模塊可以在圖形建模模塊中調用，也可以在分析算法模塊初始化時調用。
　分析算法模塊：按照整合后的電網模型，根據當前開關的狀態，分析電網元件的帶電狀態，分析結果存放在元件的帶電狀態（State）字段中，供顯示模塊使用。
顯示模塊：根據元件的帶電狀態（State）字段的內容，在電網接線圖上顯示各電網元件的帶電狀態。當元件帶電時，以繪制圖形時的顏色顯示；否則，以灰色顯示。
本文主要討論了電網拓撲分析算法及流程。在圖形建模的基礎上，提出了通過元件整合預處理過程減少參與拓撲計算的電氣元件的數量，從而提高計算速度的方法。
參考文獻
[1] 李冰劍，張學軍.電力系統網絡拓撲的分析與比較[J].科技情報開發與經濟，2011，21（1）：184-187.
[2] 林濟鏗，覃嶺，羅萍萍.基于圖形建模的電力系統拓撲分析新方法[J].電力系統自動化，2005，29（22）：54-59.
[3] 向德軍，楊銀國.基于地理信息系統的電力網絡拓撲分析[J].繼電器，2006，34（20）：20-23.