摘 要: 提出基于過飽和Hopfield神經網絡(OHNN)和驅動表的公鑰加密算法。算法以驅動表作為系統的驅動,經過函數組變換后產生隨機數,數據選擇器根據OHNN生成的混沌吸引子對隨機數作非線性選擇輸出,從而實現加密。安全性分析與仿真驗證表明,該算法構造的偽隨機序列具有良好的隨機性和復雜度,滿足密碼學的要求。
關鍵詞: 過飽和Hopfield神經網絡;混沌吸引子;驅動表
序列密碼實質上是一個密鑰流發生器,它通過將密鑰流序列與明文進行異或完成加密和解密。隨著密碼分析技術的發展和計算機計算能力的增強,傳統算法受到了很大的沖擊。Hopfield神經網絡具有非常豐富的非線性動力特性和表現在混沌動力學特性方面的復雜性,使其成為現代密碼學領域的一個熱點。本文結合OHNN和驅動表的優點,提出了一種新的序列密碼加密算法。該算法不僅避免了同步混沌通信系統中必須要求收發兩端嚴格同步的諸多麻煩和不便,而且消除了密文數據膨脹[1],解決了LFSRs時間延遲和特征多項式難選取等問題[2],此外在速度上較二者有很大的提高。
1 過飽和Hopfield神經網絡
在一個N階Hopfield神經網絡中,如果需要儲存的樣本總量大于0.14 N,則網絡中原本存在的穩定的吸引子將發生畸變,且每個狀態的收斂域都是混沌的,此時網絡擁有過飽和存貯的混沌吸引性質。這樣的網絡稱為過飽和Hopfield神經網絡,簡稱OHNN(Overstoraged Hopfield Neural Network)。在OHNN網絡中,聯結權值矩陣變化時,混沌吸引子和吸引域也隨之改變。若OHNN的神經元i的閾值用Qi表示,神經元i和神經元j之間的聯結權值用Tij表示。若神經元的狀態取0或1,則網絡的傳遞函數σ(t)為:

如果當前網絡狀態為Si(t),則其下一狀態Si(t+1)為:

3 基于OHNN和驅動表的公鑰加密算法
本文提出的基于OHNN和驅動表的加密算法由一個OHNN、一個函數組、一個數據選擇器和兩個驅動表組成。每個驅動表中都有1 024個不相同的32 bit十六進制的隨機數。該算法的結構如圖1所示。

4 仿真測試及安全性分析
4.1 隨機性測試
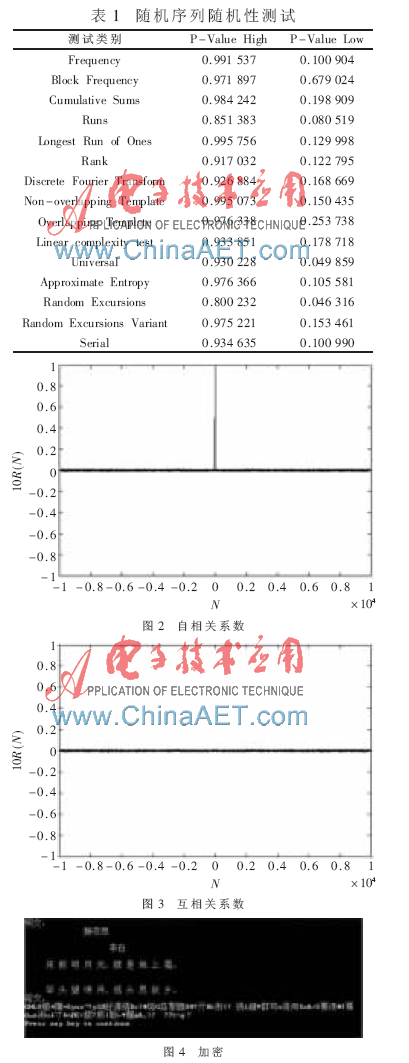
本文采用VC++6.0編程,在RedHat9.0測試平臺上依據美國國家標準與技術委員會(NIST)制定的SP800-22[5]對樣本進行測試,測試樣本為100組,每組105個數據。顯著水平α=0.01,若計算出的P-Value值小于α,則認為測試序列不為隨機序列;反之,則認為序列是隨機序列[6]。測試結果如表1所示,可以看出,算法產生的密鑰序列具有較好的隨機性。
4.2 相關性測試
選取內容重復大小合適的明文,加密后得到一份密鑰序列。隨機改變矩陣H其中的一位,加密后得到另一份密鑰序列。相關函數越小,序列的隨機性越好或越不相干[7]。測試結果如圖2和圖3所示。圖2說明序列隨機性好,圖3說明算法對初值參數敏感,一個微小的改變都可以引起雪崩效應。
4.3 加解密測試
本文對《靜夜思》進行加解密,如圖4和圖5所示。測試平臺:聯想開天M5250,CPU Intel?誖Pentium?誖3.40 GHz 3.39 GHz,內存0.99 GB,此時系統運行速度是參考文獻[2]的17倍多。

假如分析者采用窮舉法,暴力攻擊系統。由于OHNN由N個神經元所組成,每個隨機變換矩陣 H都存在N?鄞種可能,即系統的密鑰空間為N?鄞。要得到目標隨機變換矩陣,分析者需要進行N?鄞次運算。假設采用每秒鐘能計算105個變換矩陣的專業計算機,當N=32時,嘗試一次就需要1020 MIPS Years,遠遠超出了現在所能接受的安全水平1012 MIPS Years[1]。
參考文獻
[1] 劉年生,郭東輝.基于神經網絡混沌吸引子的公鑰密碼算法安全性分析及其實現[J].廈門大學學報(自然科學版),2007,46(2):187-193.
[2] 何崢,李國剛.基于神經網絡混沌吸引子的混合加密算法[J].通信技術,2012,45(5):49-52.
[3] HOPFIELD J J.Neurons, dynamics and computation[J].Physics Today,1994(47):40-46.
[4] Wu Hongjun.A new stream cipher HC-256[EB/OL].[2004].http://eprint.iacr.org/2004/092.pdf.
[5] NIST.A statistical test suit for random and pseudo-random number generators for cryptographic applications[OL].[2010].http://csrc.nist.gov/publications/nistpubs/800-22-rev1a/SP800-22rev1a.pdf.
[6] 廖曉峰,肖迪,陳勇,等.混沌密碼學原理及其應用[M]. 北京:北京科學出版社,2009.
[7] 張雪峰,范九倫.基于線性反饋移位寄存器和混沌系統的偽隨機序列生成方法[J].物理學報,2010,59(4):2289-2297.

