摘  要： 對圖像中常見的高斯噪聲特性進行了分析，對含有較強高斯噪聲的數字圖像的邊緣檢測方法進行了研究。分析了邊緣的方向性相關特征和連續性相關特征，設計了圖像特征矢量圖，檢測圖像特征矢量相關的相似度，提取出抗噪聲的圖像邊緣檢測方法。仿真驗證表明，對于含有較強高斯噪聲的圖像，本方法能夠有效抑制噪聲，而且能夠提取出準確清晰的邊緣。本算法在噪聲圖像中能很好地克服普通算子的噪聲問題，而且算法簡單，計算量較少。
關鍵詞： 高斯噪聲；噪聲圖像；邊緣檢測；矢量相關

　邊緣是圖像目標檢測主要方法，而噪聲圖像的邊緣檢測往往受噪聲影響較大，對噪聲敏感。噪聲和邊緣都屬于高頻信號，用濾波器濾除噪聲的同時也損失了圖像細節信息。如何在噪聲圖像中很好地提取邊界是圖像處理中的難點。傳統的邊緣檢測方法已經提出了一些基于模板的算法，理論分析表明，這些檢測器均屬于高通濾波器，故對含有噪聲的圖像邊緣檢測效果并不理想[1-2]。用基于小波變換的邊緣檢測方法提取邊緣可以有效地提取邊緣，但是計算量較大，為了辨識噪聲，要進行多級小波分解[3-5]。常用的微分算子有Roberts算子[6]、Sobel算子[7]、Prewitt算子[8]、Canny算子[9-10]以及LoG算子[11]等。以往的算法很少利用邊緣的方向特征以及連續性特征，邊緣具有的方向性和連續性也是區別于噪聲的顯著特征。
　本文根據邊緣區別于噪聲的特征提出了充分利用邊緣方向性顯著和邊緣強的關聯特征，提出了一種基于兩種經典的邊緣提取算子得到梯度矢量圖像，計算矢量圖像自身矢量相關度和矢量圖像之間的矢量相關度，最終確定邊緣的算法。本算法在噪聲圖像中能很好地克服普通算子的噪聲問題，而且算法簡單，計算量較少。
1 設計圖像的初始梯度矢量圖
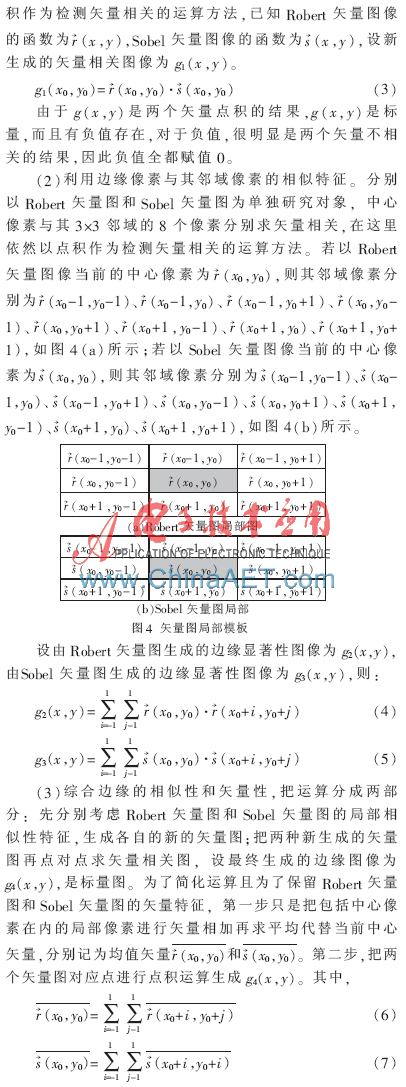
　圖像的邊緣檢測算子很多，模板越大抗噪效果越好，但檢測到的邊緣較粗，不利于邊緣定位。分析幾種常見的邊緣檢測算子，并且考慮到矢量圖像在不同的尺度下的邊緣檢測算子需要保證梯度矢量的方向特征一致性，本文選擇了2×2大小的Robert算子和3×3大小的Sobel算子，如圖1和圖2所示。

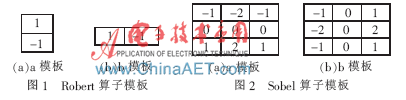
    如果兩個矢量相似，則大小和方向兩個參量都很接近，如果只有大小相似而方向不同，則說明兩個矢量的相似度并不高。由于噪聲是隨機分布的，噪聲在不同尺度的模板下所生成的梯度矢量，即使幅值相似，方向也是隨機的，因此充分利用矢量的方向特征可以有效地區分噪聲點和邊緣點。再者，邊緣一般都是連續的一些像素，而噪聲沒有連續的特征，利用與周圍像素是否存在連續性也可以區分噪聲點和邊緣點。
　本文利用邊緣梯度矢量的方向特征和連續特征可以把邊緣檢測分成3個方向來討論。
　（1）只利用方向特征。對Robert矢量圖和Sobel矢量圖進行點對點的矢量相關性運算。在這里選擇矢量的點

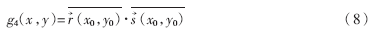
3 實驗結果分析
　實驗結果如圖5所示。實驗選取大小為256×256大小的的Lena圖像，如圖5（a）所示。實驗中，采用含有均值為0、方差為0.05的Gaussian噪聲圖像，如圖5（b）所示。圖5（c）為Robert算子提取的邊緣圖像，圖5（d）為Sobel算子提取的邊緣圖像，從實驗結果可以看出，圖像噪聲對邊緣提取有很大的影響，Robert算子對噪聲很敏感，而Sobel算子由于采用較大一點的模板，抗噪效果較好，但是還是檢測出很多噪聲點。
本文根據邊緣的方向特征和邊緣特征做了3個實驗。

　實驗1：只是把圖像對應像素進行矢量相關運算，圖5（e）為兩種梯度圖像幅值相關圖，可以看出噪聲在很大程度上得到抑制，這是因為在不同大小尺度下邊緣具有一定穩定性，而噪聲隨著模板的增大而下降；圖5（f）為兩種梯度矢量圖的矢量相關圖，與圖5（e）相比，在邊緣保持基本不變的情況下，能更好地抑制噪聲。
　實驗2：依據圖像邊緣的連續性特征，分別對Robert矢量圖和Sobel矢量圖進行局部矢量相似性計算，得到各自的連續性相關的邊緣圖像，如圖5（g）和圖5（h）所示。從實驗結果可以看出，邊緣的連續性可以很好地抑制噪聲。
　實驗3：為了把圖像邊緣的方向特征和連續特征綜合考慮，設計了實驗3，圖5（i）和圖5（j）是把Robert矢量圖和Sobel矢量圖進行局部矢量相加求均值。從實驗結果看，僅僅簡單的矢量加也可以有效地突出邊緣信息。再考慮兩種矢量圖對應點的矢量相關性，最后得到圖5（k），從最后得到的邊緣效果來看，綜合考慮邊緣特征能更好地提取邊緣，抑制噪聲。
　圖像的邊緣檢測是圖像分割的重要方法，而高斯噪聲的消除則是圖像去噪的難點。本文針對高斯噪聲提出了基于邊緣矢量相關的邊緣檢測方法，對帶有較強噪聲的圖像能夠很好地提取出清晰準確的邊緣。該算法不必先對圖像濾波平滑，直接對帶噪聲的圖像提取邊緣，為進一步圖像分割和檢測提供了更簡潔的思路。
參考文獻
[1] JIANG X， BUNKE H. Edge detection in range images based on scan line approximation[J]. Computer Vision and Image Understanding， 1999， 73（2）： 183-199.
[2] 梅躍松，楊樹興，莫波.基于Canny算子的改進的圖像邊緣檢測方法[J].激光與紅外，2006，36（6）：50-503.
[3] CHANG G， YU B， VETTERL IM. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. IEEE Transactions on Image Processing， 2000， 23（9）： 1522-1531.
[4] 吳靜進，陳巍.基于多尺度提升小波的邊緣檢測[J].重慶科技學院學報（自然科學版），2009，13（2）：95-97.
[5] MAZZAFERRI J， CAMPUS J， ESCALERA J C. Edge detect  or  tolerant to object defocuing[J]. Optics Communications， 2010， 283（19）： 3639-3645.
[6] GONZALEZ R C， WOODS R E. Digital Image Processing[M]. New Jersey： Prentice-Hall， 2008.
[7] SHIH F Y. Image processing and pattern recognition： fundamentals and techniques[J]. New Jersey： John Wiley & Sons，2010.
[8] JOHN C. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1986， 8（6）： 679-698.
[9] ZHANG Y， ROCKETT P I. The Bayesian operating point of the Canny edge detector[J]. IEEE Transactions on Image Processing， 2006， 15（11）： 3409-3416.
[10] MCILHAGGA W. The Canny edge detector revisited[J]. International Journal of Computer Vision， 2011， 91（3）： 251-261.
[11] TORRE V， POGGIO T A. On edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1986， 8（2）：147-163.