文獻標識碼: A
文章編號: 0258-7998(2014)10-0069-03
0 引言
電磁波傳播時,如果介質有突變或者不均勻,就會發生散射,其逆過程就是電磁逆散射。隨著科技不斷地高速發展,逆散射的研究應用有了明顯的實際價值與突破。當前通過應用多探測傳感器、測量手段和計算機技術,可以高效地采集到很多的電磁逆散射數據信息,并且進行保存。與此同時,還將這些數據采用科學的技術手段進行處理以及呈現出最終結果信息[1-2]。其中比較有代表性的研究有:在上世紀90年代左右,Chew以及Wang提出了一種解決了Born近似與Rytov近似的二維逆散射問題的有效方法,即是Born迭代法和變形Born迭代法;90年代中期,Lin以及Kiang研究了在衍射層析成像以及等效源背景下的一種逆散射方法,能夠確定二維導體柱的幾何形狀與方位。然而近20年,這一領域在具體的實際項目應用中卻一直未能有很好的突破,極易出現獲取數據不準確等問題[3-5]。目前為止,國內外學者采用了很多方法破解上述電磁逆散射應用中碰到的問題,1979年Schmidt等人首次給出多重信號分類(MUSIC)算法,該算法使得空間譜估計算法邁入了新的階段,是空間譜估計理論體系的核心算法[6-7]。本文引入了時間反演進行多重信號分類法(MUSIC)算法改進,實現了理想和擴展散射物圖像數據的確定。由算法應用及對比結果可知,設計算法優勢明顯,這一研究對于電磁逆散射的推廣和實際應用具有很高的借鑒價值。
1 時間反轉算法的理論模型

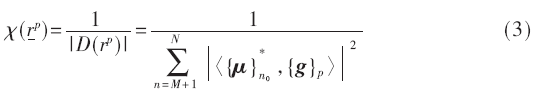
計算出的最后結果處于散射位置的最高位置。本文改進的MUSIC算法正是基于上述理論模型建立的。
2 擴展散射體的改進算法的應用設計
理想的點散射體采用改進MUSIC算法得出的結果非常好。然而,面向擴展目標物質散射體時,得出的結果還需要驗證。理論研究表明,矩陣圖的結果以及特征值的數量決定了重建圖像的結果,下面將從這一角度對不同數據進行結果分析。
2.1 Ipswich數據集的應用重建
美國的電磁測量設施在Ipswich和Massachusetts,給出了16個目標的電磁散射數據。在這些目標中,前面的3個目標里有的數據較少,無法用來重建成像;最后的3個目標里有合成數據,也無法用來重建成像。因此,只剩下10個目標可以進行分析研究,即是ips004~ips013。Ipswich數據是單一頻率的遠電場數據。它的波長λ=3 cm,發射器和接收器分別處于半徑為3.7 m和3 m的圓上。在R=3.7 m的圓上有36個發射器,每兩個發射器之間都間隔10°。此時,接收裝置有兩套,在R=3 m的圓上有36個接收器,每兩個接收器之間都間隔10°;另一套在R=3 m的圓上有1 800個接收器,每兩個接收器之間都間隔0.2°。而物體的折射率無法知曉。因為發射器與接收器距離散射體很遠,所以可看作是入射場在無窮大處發射,散射場在無窮大處散射,同時還以平面波作入射場,則有:


2.2 非均勻的介質目標圖像重建的算法應用
雙圓形金屬柱體如圖2所示。其面積是0.3 m×0.3 m,第一和第二個柱體的中心點坐標分別是(x,y)=(0,0.045)m,(x,y)=(-0.01,-0.045)m,顯然這是一類非均勻的介質目標。TE波在4 GHz下的多重靜態響應矩陣圖如圖3(a)所示,此目標在4 GHz時的特征值圖如圖3(b)所示。x軸方向代表特征值數量,y軸方向代表特征值。4 GHz頻率下采取擴展改進MUSIC算法得到的重建結果圖如圖3(c)所示,其圖顯示的面積為75 mm×75 mm。TE波在8 GHz下的多重靜態響應矩陣圖如圖4(a)所示,該目標在8 GHz下特征值圖如圖4(b)所示。x軸方向代表特征值數量,y軸方向代表特征值。在8 GHz頻率下用擴展的改進MUSIC算法得到的重建結果圖如圖4(c)所示,其圖的顯示面積也為75 mm×75 mm。TM波在18 GHz下的多重靜態響應矩陣圖如圖5(a)所示,該目標在18 GHz時的特征值圖如圖5(b)所示。其中,x軸方向表示特征值數量,y軸方向表示特征值。在18 GHz頻率下用擴展的MUSIC算法得到的重建結果圖如圖5(c)所示,該圖顯示面積也為75 mm×75 mm。


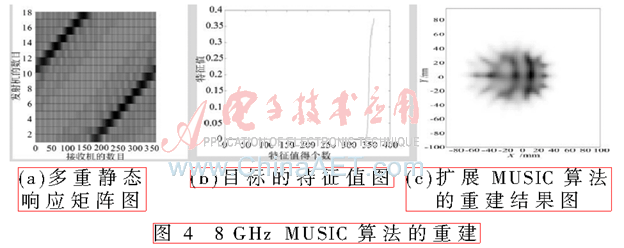
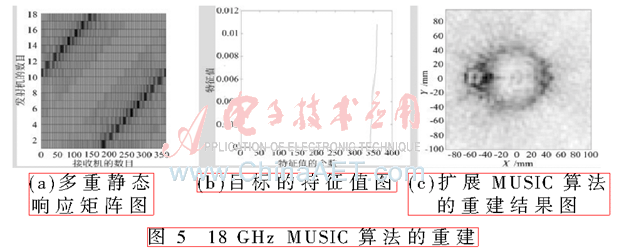
上述采用不同條件下的多頻、多收發的實測微波數據,由3種不同條件下的重建結果看出,設計算法很好地實現了解決電磁逆散射的問題,表明了引入時間反演矩陣理論的設計是準確且高效的,且對比看出頻率越高得到的重建效果越好。
3 結論
由從虛擬實驗中的重建最終數據結果可知,經過反演算法與采用線性多重信號分類算法得到的重建數據效果優勢明顯。與此同時,在面向非均勻的介質目標時改進的多重信號算法也能得出較好的結果。改進算法可以進行實時成像。文中研究對于實際推廣應用具有很高的價值。
參考文獻
[1] 歐陽華,吳正國,尹為民.dq變換和MUSIC算法在間諧波檢測中的應用[J].電力系統及其自動化學報,2013,24(5):83-87.
[2] 尤國紅,邱天爽,夏楠,等.基于均勻圓陣的擴展循環MUSIC算法[J].通信學報,2014,35(2):9-15.
[3] CHENEY M.The linear sampling method and the MUSIC algorithm[J].Inverse Problems,2001,17(4):591.
[4] CHARG?魪 P,WANG Y,SAILLARD J.An extended cyclic MUSIC algorithm[J].Signal Processing,IEEE Transactions on,2003,51(7):1695-1701.
[5] 丁衛安,馬遠良.虛擬陣列變換法解相干信號MUSIC算法研究[J].微波學報,2008,24(2):27-30.
[6] SWINDLEHURST A L,KAILATH T.A performance analysis of subspace-based methods in the presence of model errors.I.The MUSIC algorithm[J].Signal Processing,IEEE Transactions on,1992,40(7):1758-1774.
[7] KIRSCH A.The MUSIC-algorithm and the factorization method in inverse scattering theory for inhomogeneous media[J].Inverse Problems,2002,18(4):1025.

