文獻標識碼: A
文章編號: 0258-7998(2015)06-0121-04
0 引言
滑模控制器具有良好的魯棒穩定性和快速的瞬態響應[1],常被應用于線性和非線性的控制系統中,尤其是在DC-DC變換器這種變結構的開關電源結構中,滑模控制器能夠充分發揮其魯棒性和良好的瞬態響應[2]。但在實際應用中,要獲得理想的滑模控制器是不太可能的,畢竟這要求其開關頻率fs要達到兆赫級別甚至是無窮大(理想的滑模控制器的開關頻率是無窮大,一般所研究的基本上是以準滑模為主)。在分析開關電源中知道,fs過大時,開關損耗很大并會產生嚴重的電磁干擾等很多不利因素[3]。
基于以上問題,一些學者提出了滯環滑模調制技術(Hysteresis-Modulation,HM),這種方法在一定程度上降低開關頻率的同時保持了滑模控制器具有較好的魯棒性和瞬態響應,但當滯環調制負載或者是輸入電壓發生變化時,都會引起開關頻率 fs的變化,這使得其很難直接應用在DC-DC變換器中[4]。
本文針對BUCK變換器,根據滯環滑模和現有定頻滑模控制的不足,提出一種附加積分的定頻滑模控制技術,采用二階滑模面并根據標準二階系統設計滑模系數,分析附加積分項對滑模運動存在條件的影響,分析了附加積分項對消除穩態誤差和提高系統動態性能的影響。
1 BUCK變換器定頻滑模控制
1.1 定頻滑模控制器設計
圖1所示控制框圖為采用二階滑模面的典型滑模控制結構圖,圖中選用的控制器為滯環滑模控制器,雖然滯環滑模的輸出不能直接作用到BUCK變換器中,但這并不妨礙以此為基礎推導BUCK變換器的等效滑模控制函數,即定頻滑模控制器。
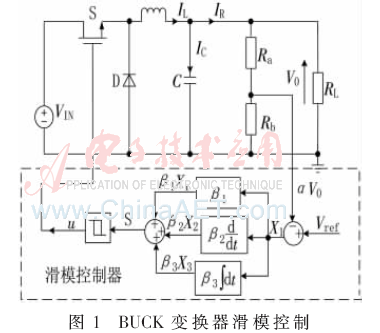
根據圖1可以得出,典型的二階滯環滑模控制器選擇受控量的誤差x1、受控量誤差的導數x2和受控量誤差的積分x3作為狀態變量。可以首先定義變換器的狀態變量x如式(1)~式(4)所示,在式(1)~式(3)中代入了BUCK變換器的數學模型。根據式(1)~式(3)可以得到BUCK變換器的狀態空間方程,狀態空間方程如式(5)所示。

由于式(7)所示滯環滑模控制函數無法直接應用在BUCK變換器中,需要得到和式(7)等效的控制函數,使滑模控制器不再采用滯環調制方式,而是采用PWM方式。根據文獻[1]提出的理論,滑模控制器的離散輸入信號u可以用連續平滑函數所替代,這個連續平滑函數就是輸入信號u的等效控制函數ueq。根據文獻[2]提出的理論,在高開關頻率下等效控制信號和電力電子變換器的占空比作用是等價的。因此可以根據上述理論推導定頻滑模控制器的占空比函數。
根據文獻[1],令滑模軌跡的導數等于零,即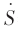 =0,從而推導出等效控制函數和占空比函數。
=0,從而推導出等效控制函數和占空比函數。
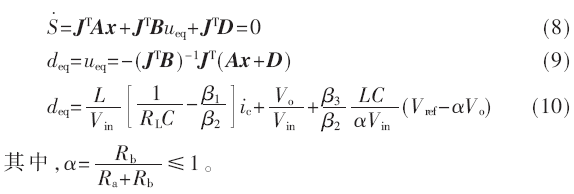
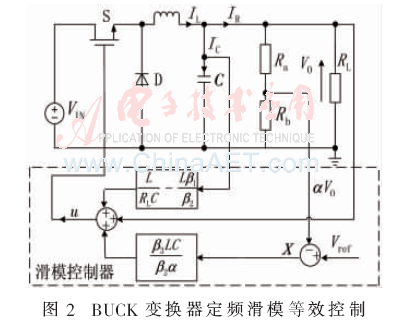
根據式(8)~式(10)可以得到,占空比函數0<deq<1,并且占空比函數代表了滯環滑模控制函數的平均值。根據文獻[2],定頻滑模控制和滯環滑模控制在平均開關頻率相等并且滑模系數完全一致的情況下,具有相同的動態響應特性。而定頻滑模控制具有開關頻率固定的優勢。圖2給出了BUCK變換器定頻滑模等效控制框圖,在圖2中,占空比函數是由式(10)決定的。
1.2 滑模存在條件
在滑模控制器中,滑模系數的取值范圍必須使滑模運動滿足存在條件[2]。為了保證滑模運動的存在性,滑模控制器的局部可達性條件必須得到滿足,即式(11)應該得到滿足:

將式(5)~式(7)分別代入到式(12)、(13)中,并將式(12)、(13)進行聯立,可以得到滑模運動的存在條件如下所示:
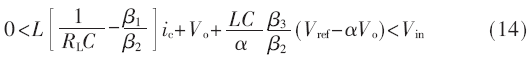
1.3 滑模系數設計原則
設計滑模系數時,首先限定其取值范圍能夠滿足滑模運動存在條件,然后在限定取值范圍內根據期望的控制器動態響應性能設計滑模系數。根據Ackermann公式,可以令滑模軌跡S=0,如式(15)所示,然后將滑模軌跡方程等效變換為標準二階系統,根據二階標準系統設計滑模系數。

2 附加積分定頻滑模控制
為了消除輸出電壓的穩態誤差,可以將穩態誤差的積分項添加到等效控制函數中,積分項一方面校正輸出電壓的穩態誤差,另一方面也加快了輸出電壓的響應速度。因此,定頻滑模控制器附加積分項的系數應該依據輸出電壓的動態響應特性來設計。附加積分定頻滑模控制器結構框圖如圖3所示。
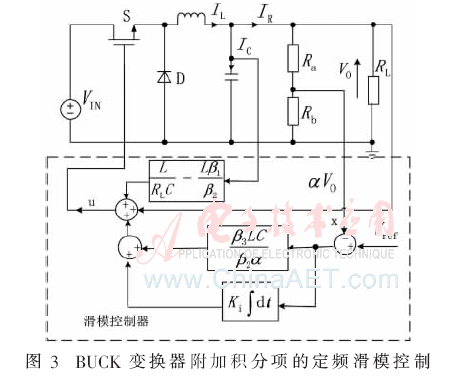
根據圖3可以得到附加積分定頻滑模控制器的等效控制函數如式(20)所示。
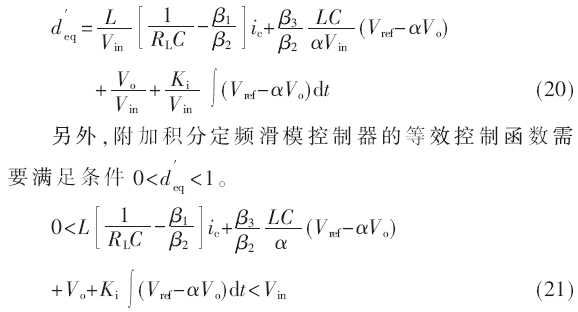
3 滑模到達階段指數趨近律
為了改善滑模到達階段的趨近運動品質,選擇定頻滑模控制器的指數趨近規律,使滑模軌跡滿足式(22),推導此時的占空比控制函數。

將式(5)、式(6)帶入式(22)可以得到占空比控制函數的表達式式(23),此時的占空比控制函數包含了3個基本項:等效控制項deq、線性控制項dL和非線性控制項dN。

對于附加積分定頻滑模控制器,同樣可以得到基于指數趨近律的占空比控制函數,如式(24)所示。

采用指數趨近律的附加積分定頻滑模控制器應用在BUCK變換器中完整控制結構框圖如圖4所示。
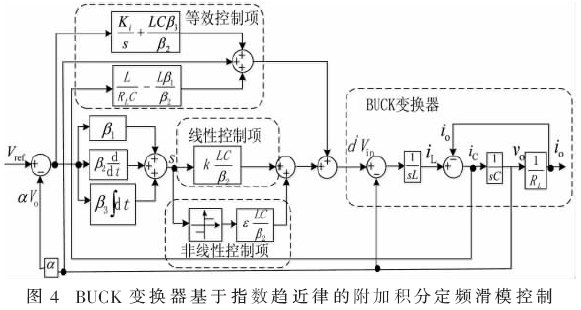
4 仿真結果與分析
通過仿真對本文所提控制方法和理論分析進行了驗證,根據以上所述的理論推導,選取的電路參數和控制參數如表1所示。
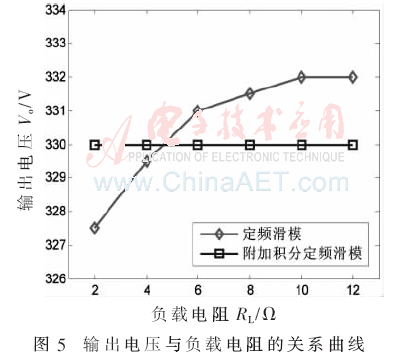
在本文中,圖5給出了定頻滑模控制與附加積分定頻滑模控制輸出電壓隨負載變化關系曲線。由圖5可以直接得出,定頻滑模控制在負載RL=2 Ω時,輸出電壓和理想輸出電壓具有2.5 V的誤差,重載情況下輸出電壓較小,隨負載逐步減輕,輸出電壓緩慢上升,所以利用定頻滑模控制時,其輸出電壓受輸出負載的影響較大。而附加積分定頻滑模控制輸出電壓不受負載電阻影響,這實現了輸出穩態誤差。在負載發生突變時,不會對電路輸出產生影響。
5 結論
本文針對BUCK變換器,設計了一種附加積分項的定頻滑模控制器,介紹了這種控制器的設計方法,通過本文的理論分析和仿真實驗驗證,可以得出如下結論:
(1)滯環滑模控制器難以直接應用在BUCK變換器中,要實現無穩態誤差輸出,定頻滑模控制器是不可能做到的;
(2)附加積分定頻滑模控制器將輸出電壓的誤差直接反映在變換器的等效控制函數中,使變換器輸出電壓不受負載電阻影響,實現了無穩態誤差的輸出。
參考文獻
[1] TAN S C,LAI Y M,TSE C K.General design issues of sliding mode controllers in DC-DC converters[J].IEEE Transactions on Industrial Electronics,2008,55(3):1160-1173.
[2] Shi Yong,Yang Xu.Zero-voltage switching PWM three-level full-bridge DC-DC converter with wide ZVS load range[J].IEEE Transactions on Power Electronics,2013,28(10):4511-4524.
[3] 張黎,丘水生.Buck變換器的積分重構滑模控制[J].電機與控制學報,2006,10(1):93-96.
[4] 許飛,馬皓,何湘寧.新型Buck逆變器3階滑模控制策略[J].中國電機工程學報,2009,29(12):41-46.

