文獻標識碼: A
文章編號: 0258-7998(2015)01-0050-03
0 引言
微機電系統(Micro Electro Mechanical Systems,MEMS)陀螺儀已經廣泛應用于慣性導航、組合導航系統中[1]。但是目前低成本MEMS陀螺儀精度相對較低,零偏穩定度等性能較差,而作為導航應用對MEMS陀螺儀的精度要求較高,因此,在使用前首先要對隨機誤差進行處理[1]。
處理這個問題的思路一般是首先建立輸出的誤差模型,再根據一定的濾波技術,通常是Kalman濾波[2],或小波變換等濾波方法[3]來估計和補償陀螺誤差。以前的相關工作一般在對單一型號陀螺儀進行分析的基礎上,建立AR模型來近似描述誤差[3-5],取得了一定的濾波效果。然而,低成本MEMS陀螺誤差成分復雜,不同低成本MEMS陀螺之間一致性差,啟動重復性差[6]。因此,難以對低成本MEMS陀螺建立準確的誤差模型,對一個陀螺的建模也無法適用其他陀螺。
為解決對低成本MEMS陀螺建模困難的問題,本文從工程實際應用角度出發,使用Allan方差法分析了MEMS陀螺儀輸出的特點,詳細探討了一種普遍適合低成本MEMS陀螺儀的實用隨機誤差實時處理方法。該方法由零偏補償、可去除粗大誤差的平均濾波算法和基于最小二乘法預測的Kalman濾波器三部分共同組成。其中,傳統Kalman濾波算法需要建立誤差模型以寫出系統狀態方程,本文所述方法不同于傳統方法,可以不對誤差進行建模,具有更好的通用性。實驗結果證明,該方法可以有效濾除噪聲,并具有良好動態特性。
1 基于Allan方差的陀螺誤差分析
為獲得低成本MEMS陀螺儀輸出的誤差特性,首先設計實驗條件采集數據并保存,然后根據文獻[7、8]中所描述的Allan方差分析法對數據進行分析。
1.1 數據采集
選取若干同一型號低成本MEMS三軸陀螺儀,該型號陀螺儀以數字量輸出,AD位數為16位。在恒溫并且將器件固定的條件下每一枚器件進行兩次上電數據采集。每次上電首先預熱30 min,然后保存數據。采樣率設置為100 Hz,每次保存15 min數據。
1.2 使用Allan方差分析法分析數據
Allan方差分析法可以確定產生數據噪聲的基本隨機過程特性,并能識別給定噪聲的來源[8]。Allan方差的計算公式為[7]:
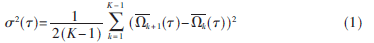
式中,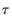 表示平均時間,K為所劃分的子集個數,
表示平均時間,K為所劃分的子集個數, 為第k個子集的平均值。按照式(1)計算每個平均時間的Allan方差,以雙對數曲線畫出Allan標準差隨平均時間變化的情況。任選一個器件兩次上電測試的原始數據,繪制雙對數曲線,如圖1所示。
為第k個子集的平均值。按照式(1)計算每個平均時間的Allan方差,以雙對數曲線畫出Allan標準差隨平均時間變化的情況。任選一個器件兩次上電測試的原始數據,繪制雙對數曲線,如圖1所示。
選取器件的X軸,分別計算測試數據的均值和均方差,計算結果如表1所示。

利用文獻[7]中所描述的分析方法對圖1和表1進行分析可知,該型號陀螺儀輸出隨機漂移中,角度隨機游走占據主要部分;同一器件不同測量軸誤差特性各不相同;同一個陀螺儀兩次上電的誤差特性并不相同。
由于采用16位AD,原始輸出序列的范圍在-32 768~
32 768之間,通過觀察,發現數據中偶爾存在一些明顯錯誤的野值,例如,一段實測原始輸出序列為67,49,
55,-233,21,17,23,63。可以發現,數據-233明顯不合理,屬于野值,這種野值一般不會在連續10個采樣中出現兩次。
2 實時濾波算法
由分析的結果可以發現難以建立一個通用的陀螺誤差模型。因此,對誤差建模的方法并不適用于低成本MEMS陀螺儀。針對低成本MEMS陀螺輸出特點,本文設計了一種實時濾波算法,該方法分為三個步驟。
2.1 零偏補償
在進行濾波之前,首先應該去除原始測量值中的常值漂移信號[1]。文獻[1]指出,可以用一段零輸入條件下輸出數據的均值代表整體的零偏。經充分預熱后,在敏感軸上零角速度輸入,保存一定時間的數據。對這段數據求均值,作為陀螺儀輸出的零偏,在以后每次得到的原始值都減去這個零偏。
2.2 平均濾波算法
對已去除零偏的原始數據,由于存在粗差,應先設法抑制。
首先,用陀螺儀以往的幾個測量值的均值作為下一次實際值的估計[5],均值估計法的表達式為:

式中,xi為數據窗內的元素,L為數據窗的長度, 為均值估計結果。由于不是滑動平均方式,經過平均后,
為均值估計結果。由于不是滑動平均方式,經過平均后,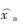 的輸出率為xi輸出率的1/L,L越大,輸出率越低。
的輸出率為xi輸出率的1/L,L越大,輸出率越低。
通過觀察原始數據可以發現,野值一般不會在短期內連續出現,野值和正常值的偏差在200以上。因此,本文選取L=5,對5個歷史數據平均得到估計結果 ,再設置一個門限值q,然后將5個歷史數據xi分別和
,再設置一個門限值q,然后將5個歷史數據xi分別和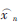 做差,用差值的絕對值和q比較,如果大于q,則xi被判決為野值,否則為有效數據。實際使用時,L和q應根據需要靈活選取。最后,將剩下的有效數據xi再次用式(2)計算均值,作為平均濾波后的結果輸出。經過平均濾波后的輸出序列不僅消除了粗大誤差的影響,方差也顯著降低。
做差,用差值的絕對值和q比較,如果大于q,則xi被判決為野值,否則為有效數據。實際使用時,L和q應根據需要靈活選取。最后,將剩下的有效數據xi再次用式(2)計算均值,作為平均濾波后的結果輸出。經過平均濾波后的輸出序列不僅消除了粗大誤差的影響,方差也顯著降低。
2.3 基于最小二乘法預測的Kalman濾波算法
在經過平均濾波算法后,將輸出再經過Kalman濾波器進一步處理。
Kalman濾波是工程中應用的成熟方法,其工作過程可以分為預測和校正兩個過程[9]。預測過程在上一個歷元狀態估計值的基礎上,利用系統的狀態方程來預測當前歷元的狀態值,即先驗估計值。涉及公式如下:

校正過程利用實際測量值來校正經上一步預測得到的狀態先驗估計值,獲得后驗估計值。涉及公式如下:

對于預測過程,由于無法對低成本MEMS陀螺儀誤差建立通用、準確的模型,不能采用傳統的建立AR模型預測的方法,但并不意味著無法對當前輸出值做出先驗估計。載體運動具有連續性和運動變化的緩慢性[9],這意味著載體具有保持原來運動狀態的趨勢,在短時間內的真實角速度不會發生突變。最小二乘法通過最小化誤差的平方和尋找數據的最佳函數匹配,利用最小二乘法可以簡便地根據歷史記錄數據估計下一時刻的真值,并使得估計數據和真實數據誤差的平方和最小。
另外,最小二乘法直接根據歷史后驗估計值實時調整參數,來預測下一時刻的實際值,是一種動態的預測方法,這樣不僅適用于靜止條件下的濾波,在有角速度輸入變化的情況下依然可以有效工作。
本文設置一個深度為10的FIFO,用于保存Kalman濾波后驗估計值輸出結果。FIFO內為按時間先后順序排列的最近的10個濾波后輸出結果。對于一般的應用場景,在短時內載體不可能發生劇烈的運動狀態變化,數據序列具有穩定性,擬合的結果近似為一條直線。為保證預測準確性并兼顧計算復雜度,使用二次函數擬合,令:

式中,ti為時間序列;xi為對應的后驗估計值,即實際使用值;a、b、c為擬合二次函數的參數,此時為未知。令:

其中, 為利用式(8)計算得到的每一時刻的估計值,是未知參數的函數,分別與實際值作差。?追為這些差的平方和。根據最小二乘法原理,?追應取得最小值。用函數?追對a、b、c求偏導數,令偏導數等于0,獲得關于a、b、c的線性方程組,解方程確定未知參數,代入式(8),可得:
為利用式(8)計算得到的每一時刻的估計值,是未知參數的函數,分別與實際值作差。?追為這些差的平方和。根據最小二乘法原理,?追應取得最小值。用函數?追對a、b、c求偏導數,令偏導數等于0,獲得關于a、b、c的線性方程組,解方程確定未知參數,代入式(8),可得:

使用式(10)即可獲得當前時刻的先驗估計值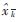 ,式(10)也即系統狀態方程。另外,預測過程除了獲得預測值,還需要一個衡量預測值可靠性的過程噪聲參數Q。由于預測值將在校正過程中被校正,將校正后的使用值序列和預測值序列做差分,差分序列的方差即表示預測結果的可靠性。即:
,式(10)也即系統狀態方程。另外,預測過程除了獲得預測值,還需要一個衡量預測值可靠性的過程噪聲參數Q。由于預測值將在校正過程中被校正,將校正后的使用值序列和預測值序列做差分,差分序列的方差即表示預測結果的可靠性。即:

對于校正過程,根據去除粗大誤差后,由式(2)計算得到的平均濾波結果,作為校正過程的測量值輸入。測量噪聲R用平均濾波后的數據方差衡量,即:

調整合適的狀態均方差初始估計值P0,保證濾波器收斂。以Kalman濾波后的校正值作為使用值輸出,完成對陀螺輸出的濾波。
3 濾波器性能測試
為不失一般性,再選一顆該型號MEMS陀螺儀的輸出數據,使用上述濾波方法對數據進行實時處理。為描述動態下的濾波性能,可以使用在所采集的靜態數據基礎上疊加一個角速率來模擬動態變化[2]。
3.1 靜態實驗
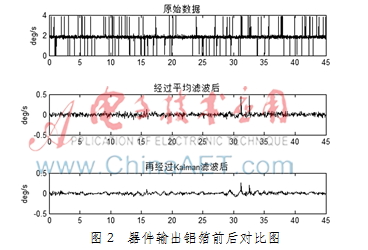
截取一段時間數據作圖,圖2展示陀螺濾波前后的輸出對比。
由圖2看出,雖然原始輸出的零偏和波動性相差很大,圖形上有較密集的毛刺,但是在經過常值漂移補償,平均濾波算法后,輸出零偏有效改善,毛刺被基本濾除,粗大誤差得到了有效抑制。在此基礎上,Kalman濾波器進一步改善了零偏穩定度,獲得了更出色的濾波降噪效果。將這段數據的均值和均方差進行定量計算,如表2所示。

由表2看出,經過濾波,能使零偏減小到令人滿意的程度,同時,均方差在濾波后小于濾波前的十分之一,證明輸出序列的波動性被顯著降低,零偏穩定度性能得到大幅提升。
3.2 動態實驗
選取另一顆陀螺儀采樣,首先截取90 s靜態實驗數據,以一次函數擬合模擬勻角加速度轉動過程;以常數模擬勻角速度轉動;以正弦函數模擬較為復雜角速度變化情況。圖3為模擬信號、與原始數據疊加后信號和濾波后信號對比圖。
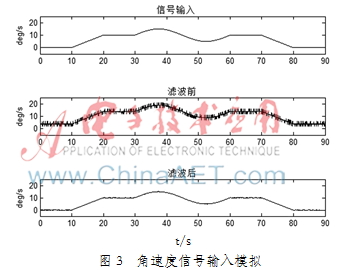
由圖3看出,濾波后,零偏被有效校正,方差明顯降低,輸出較完美地恢復了輸入信號,證明該方法在動態下依然可以有效工作,工程實際應用價值較高。
4 結論
低成本MEMS陀螺儀特性參差不齊,啟動重復性差,不適宜采用對誤差建模的方法處理隨機誤差。本文所述實時濾波算法從實際工程應用角度出發,可以較好地抑制低成本MEMS陀螺隨機誤差中的角度隨機游走,有效補償常值漂移,均方差小于濾波前的十分之一,大幅提升低成本MEMS陀螺儀零偏穩定度性能。該方法不僅能在靜態下工作,在動態情況下不會淹沒有效信號,也表現出良好性能。另外,該方法相對易于實現,算法復雜度相對低,普遍適用于低成本MEMS陀螺儀的隨機誤差濾波,具有較高的實用價值。
參考文獻
[1] 蒙濤,王昊,李輝,等.MEMS陀螺誤差建模與濾波方法[J].系統工程與電子技術,2009,31(8):1944-1948.
[2] 錢華明,夏全喜,闕興濤,等.基于Kalman濾波的MEMS陀螺儀濾波算法[J].哈爾濱工程大學學報,2010,31(9):1217-1221.
[3] 叢麗,秦紅磊,邢菊紅.小波閾值去噪和FAR建模結合的MEMS陀螺數據處理方法[J].電子技術應用,2010,36(12):120-123.
[4] 陳濤,王新龍,杜宇.基于AR模型的光纖陀螺建模方法研究[J].魚雷技術,2005,13(3):25-27.
[5] 吉訓生,王壽榮.MEMS陀螺儀隨機漂移誤差研究[J].宇航學報,2006,27(4):640-642.
[6] 張智永,周曉堯,范大鵬.穩定平臺中陀螺漂移自適應實時估計算法[J].航空學報,2012,33(6):1044-1051.
[7] 趙思浩,陸明泉,馮振明.MEMS慣性器件誤差系數的Allan方差分析方法[J].中國科學,2010,40(5):672-675.
[8] 王新龍,李娜.MEMS陀螺隨機誤差的建模與分析[J].北京航空航天大學學報,2012,38(2):170-174.
[9] 謝鋼.GPS原理與接收機設計[M].北京:電子工業出版社,2009:129-134.

