摘 要: 針對現有的網絡安全態勢預測方法沒有從影響網絡安全態勢的安全因子入手,不能準確地預測未來網絡安全態勢,提出了一種基于灰色理論和BP神經網絡的預測方法。首先依據灰色模型系數的取值大小選擇最合適的背景值,并構造了一種新的模型背景值函數。其次,結合GM(1,1)、GM(1,N)模型預測網絡安全態勢,并用BP神經網絡對態勢預測值進行修正。最后,通過真實的網絡環境驗證了所提出的方法在網絡安全態勢預測中的有效性。
關鍵詞: 灰色理論;網絡安全態勢感知、預測;BP神經網絡;粒子群算法
0 引言
隨著網絡信息技術的日益發展,互聯網正在成為社會的信息基礎設施。同時,網絡攻擊和破壞行為日益普遍,傳統的網絡安全防護設備(如防火墻、IDS等)功能單一、不能全方位地對網絡的安全狀態做出整體的評價和估計[1]。網絡安全態勢感知就是在這種背景下產生的。其中網絡安全態勢預測作為網絡安全態勢感知的一個重要部分,它能夠對網絡系統整體運行的安全趨勢進行把握,實時地感知網絡所面臨的威脅;為及時、準確的決策提供可靠依據,使由網絡不安全帶來的風險和損失降低到最低限度。
目前存在多方位、多層面的預測方法和模型,主要有:灰色GM(1,1)模型[2]、神經網絡[3]、支持向量機(Support Vector Machine,SVM)[4]等。
上述預測方法都在一定程度上對網絡安全態勢進行了預測,存在的問題總結如下:預測方法僅從網絡歷史的整體安全態勢本身數據進行分析,忽略影響網絡安全態勢的安全因子[5],而實際上安全態勢的變化是與安全因子的變化密切相關的。
對此,本文從影響網絡安全態勢的安全因子入手,結合灰色GM模型、BP神經網絡預測網絡安全態勢,并通過真實的實驗環境去驗證本方法的準確性。
1 網絡安全態勢安全因子
在互聯網實際應用中,本文從網絡基礎運行性、網絡脆弱性、網絡威脅性[6]劃分安全因子。脆弱性側重描述網絡本身的安全漏洞。因子包含:子網內安全設備數目、關鍵設備開放端口的數量、關鍵設備漏洞數目。網絡基礎運行性主要指網絡本身的運行狀態,能直接反映安全事件造成的影響。因子有:主機CPU、內存等資源消耗量、子網流量增長率、子網數據流總量、子網帶寬占用率、數據丟包率。威脅性側重描述各種網絡攻擊對網絡內部產生的危害程度,主要統計已知攻擊、疑似攻擊和惡意代碼的數量、頻率及危害度。因子包括:報警數目、惡意代碼數量、病毒木馬等的攻擊頻率、數目及危害度。
2 灰色預測模型
灰色理論[7]主要通過對部分已知信息的生成、開發、提取有價值的信息、實現對系統運行規律的正確認識從而達到科學的預測。
2.1 灰色GM(1,1)、GM(1,N)模型
灰色預測模型中最基本的是GM(1,1)模型,其預測的灰色微分方程為:
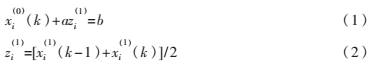
(i=1,2,…N,k=1,2,…n)
其中,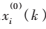 為數據序列,
為數據序列,![77R79Z1W~TQR]98PNIU4A60.png 77R79Z1W~TQR]98PNIU4A60.png](http://files.chinaaet.com/images/2016/02/13/6359098543823792574875052.png) 為
為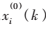 的累加生成序列,a為發展系數,b為灰色作用量;
的累加生成序列,a為發展系數,b為灰色作用量;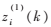 模型背景值。讓
模型背景值。讓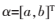 ,按最小二乘法擬合得
,按最小二乘法擬合得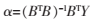 。其中:
。其中:
![FW{0Z)I%7559P7821ONES]R.png FW{0Z)I%7559P7821ONES]R.png](http://files.chinaaet.com/images/2016/02/13/6359098563551392573996319.png)
GM(1,N)模型是一種適合于建立各因子變量的動態關聯分析模型,含N個因子序列的預測灰色微分方程為:
![YT2H]3)_}XWWPYLJ0CC)3Z7.png YT2H]3)_}XWWPYLJ0CC)3Z7.png](http://files.chinaaet.com/images/2016/02/13/6359098583730192573957433.png)
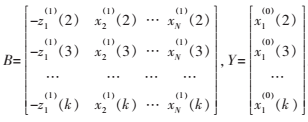 參數向量
參數向量0)WHU$Q4[ZN0](8RWK.png](http://files.chinaaet.com/images/2016/02/13/6359098595385592579587096.png) 可由B、Y按最小二乘法計算,微分方程的離散解為:
可由B、Y按最小二乘法計算,微分方程的離散解為:
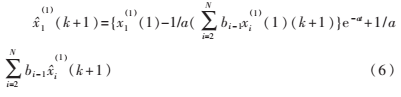
對式(6)累減還原得 擬合預測值。
擬合預測值。
2.2 灰色背景值的改進
上述模型的背景值[8]函數 采取均值生成方法構造。而實際是在[k-1,k]上對式
采取均值生成方法構造。而實際是在[k-1,k]上對式![VKQB(FOZRIE9VTKR]J3QN7W.png VKQB(FOZRIE9VTKR]J3QN7W.png](http://files.chinaaet.com/images/2016/02/13/6359098618680992574819771.png) 兩邊求積分。二者之間的差值是灰色模型精度不高的主要原因;參考文獻[9]在序例具有高指數規律的情況下,得到新的背景值構造公式為:
兩邊求積分。二者之間的差值是灰色模型精度不高的主要原因;參考文獻[9]在序例具有高指數規律的情況下,得到新的背景值構造公式為:

基于此,本文設定:
當0<-a≤0.3,序列變化平穩時,采取均值生成方法構造背景值函數。
當0.3<-a≤0.8,序列變化呈中間狀態時,采用本文構造的背景值:
![]713I02GM2X8OYAPOK(KEQP.png ]713I02GM2X8OYAPOK(KEQP.png](http://files.chinaaet.com/images/2016/02/13/6359098628502592579945352.png)
參數l1、l2、l3由粒子群算法進行優化。
當0.8<-a≤1時,原始序列呈高指數增長,選取新背景值構造函數。
3 結合灰色理論和BP神經網絡的預測原理
灰色理論具有建模簡單、運算方便等特點。神經網絡具有自學習、自組織和自適應能力,對非線性數據的處理能力較弱,神經網絡的特點恰好能對灰色模型進行補充。因此,以灰色模型的貧信息代替神經網絡所需的大樣本,以BP神經網絡的非線性處理能力彌補灰色模型非線性擬合差的缺點,建立性能更優的灰色神經網絡模型。
預測算法步驟如下:
(1)對歷史安全因子、網絡安全態勢歷史序列無量綱歸一化處理。計算發展系數a,依據a的大小選擇對應的模型背景值函數。
(2)將安全因子數據輸入到GM(1,1)模型中,得到安全因子預測值![@~R)6%[V]K6XG`LU1ZA4L]7.png @~R)6%[V]K6XG`LU1ZA4L]7.png](http://files.chinaaet.com/images/2016/02/13/6359098635150992571073961.png) 。
。
(3)結合歷史網絡安全態勢值,將安全因子所有預測值輸入到GM(1,N)模型中,得到網絡安全態勢預測值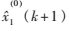 、殘差
、殘差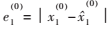 。
。
(4)確定訓練樣本、預測樣本數目,以安全因子序列所有預測值輸入BP神經網絡的輸入端、殘差作為輸出結果、所有訓練樣本通過BP神經網絡的均方誤差為目標對BP神經網絡進行訓練。最后用訓練好的BP神經網絡對殘差進行預測,得到殘差預測值 。
。
(5)對預測結果進行殘差修正,輸出最終網絡安全態勢預測值:
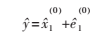 (9)
(9)
4 粒子群算法優化模型背景值參數
4.1 粒子群算法
PSO粒子群算法屬于帶有全局策略和啟發性質的群體智能進化計算方法。每個優化問題的可行解都是搜索空間中的一個粒子。算法首先隨機生成一個粒子種群,然后追隨當前最優粒子在種群中進行迭代搜索,直到達到要求,停止搜索。種群粒子的速度、位置進化公式如下:
vid(t+1)=vid(t)+c1×rand()×(pbest-xid(t))+c2×rand()×(Gbest-xid(t))(10)
xid(t+1)=xid(t)+vid(t)(11)
其中,vid是粒子的速度,維數為i×d維,c1、c2為學習因子,分別調節飛赴自身和鄰居的步長,rand()是介于(0,1)之間的隨機數,xid(t)是粒子當前位置,pbest(t)代表粒子當前最好位置,Gbest(t)代表種群當前最好位置,即全局最優位置。
4.2 PSO算法優化背景值參數的步驟
算法設計思想:將背景值的所有參數映射成種群個體的位置。設定采用的適應度函數(本文為灰色GM(1,N)模型殘差平方和的倒數![LTLRWW}I%}Q{]A0S2`)Y`]6.png LTLRWW}I%}Q{]A0S2`)Y`]6.png](http://files.chinaaet.com/images/2016/02/13/6359098661988692579662916.png) 。搜尋使適應度滿足要求的粒子位置,新生成的個體位置還原為背景值的參數,得到背景值最優參數組合。
。搜尋使適應度滿足要求的粒子位置,新生成的個體位置還原為背景值的參數,得到背景值最優參數組合。
算法步驟如下:
(1)隨機初始化背景值參數l1、l2、l3。
(2)背景值參數映射為PSO種群粒子位置向量。
(3)隨機產生初始化種群(包括隨機種群數目M、速度、位置)。
(4)依據粒子群算法更新粒子的速度和位置,得到新的粒子位置和速度。
(5)計算粒子位置映射的背景值參數、殘差和適應度。
(6)判斷適應度是否滿足設定值,如果滿足,輸出當前位置所對應的背景值參數,終止迭代;否則,繼續下一步。
(7)比較粒子的當前位置和歷史最優位置,若當前位置較好,用當前位置替換歷史最優位置;然后將粒子的個體最好位置與全局最優位置做比較,若粒子的個體值更好則記錄此位置為新的全局最優位置。
(8)迭代次數t=t+1,如果t>Tmax,終止迭代,否則,轉到第(4)步。
通過PSO粒子群算法,搜尋到最優的背景值參數組合,使灰色GM(1,N)模型的殘差最小,從而得到精度最好的模型。
5 實驗分析
實驗前本文采用參考文獻[10]的態勢評估方法結合安全因子對網絡安全態勢先進行評估,以便獲取實驗所需的網絡安全態勢數據。
5.1 實驗準備
本文搭建了由主機、路由器、交換機、服務器等組成的網絡進行實驗。
網絡中包含的受攻擊目標分別為Web服務器、備份數據庫、主數據庫、DNS服務器、TCP服務器。實驗過程中的數據來源于路由器中的Snort入侵檢測信息、Netflow數據流信息、主機的Nessus漏洞掃描信息、Firewall日志信息。實驗時將SQL注入漏洞攻擊數據庫、SYN Flood攻擊TCP服務器、Web服務器、UDP Flood攻擊DNS服務器等,然后從網絡節點獲得所需的異常數據,在MATLAB7.0平臺進行仿真實驗。
實驗參數:設定預測周期為12 h,即通過前11個時間段的態勢值預測之后的1個時間段的態勢值,選取訓練樣本數為101,預測樣本數為23。本次的粒子群算法中,粒子種群初始規模M設定為100,位置xid∈[0,1]、速度vid∈[-100,100],最大迭代次數Tmax=1 000、學習因子c1、c2均為2,適應度設定為:1 000。對比不經任何優化處理的灰色GM(1,1)模型、BP神經網絡對網絡安全態勢進行預測。
5.2 實驗結果
預測結果曲線圖如圖1所示。
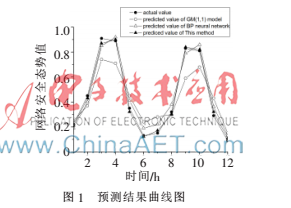
可以進一步通過對模型得到的預測值計算殘差、相對殘差、檢驗模型的準確性。表1為精度檢驗結果。

5.3 結果分析
從網絡安全態勢預測結果可以看出,3種方法檢驗結果誤差各有不同:灰色GM(1,1)只能粗略地反映網絡安全態勢的總體趨勢;BP神經網絡預測結果誤差相對GM(1,1)模型小,但是其訓練樣本過大,訓練時間較長;對比GM(1,1)模型、BP神經網絡,本方法預測精度更高。
6 結論
本文的方法在實際應用中有兩方面的難點:一是預測結果網絡安全因子的限制,如果選取的安全因子不完全,會很大地影響網絡安全態勢的預測結果,二是預測能力受安全因子預測能力的影響,因而如何提高安全因子預測的準確性將是下一步的工作重點。
參考文獻
[1] 王庚,張景輝,吳娜.網絡安全態勢預測方法的應用研究[J].計算機仿真,2012,29(2):98-101.
[2] 鄧聚龍.灰理論基礎[M].武漢:華中科技大學出版社,2002.
[3] 謝麗霞,王亞超,于巾博.基于神經網絡的網絡安全態勢感知[J].清華大學學報,2013,53(12):1751-1760.
[4] 汪材印.灰色關聯分析和支持向量機相融合的網絡安全態勢評估[J].計算機應用研究,2013,30(6):1859-1862.
[5] 葉健健,文志誠,吳欣欣,等.基于多層次數據融合的網絡安全態勢分析方法研究[J].微型機與應用,2015,34(8):5-7,11.
[6] 孫德衡.基于指標融合的網絡安全態勢評估模型研究[D].西安:西北大學,2012.
[7] 劉思峰,謝乃明.灰色系統理論及其應用[M].北京:科學出版社,2008.
[8] 劉思峰,鄧聚龍.GM(1,1)模型的適應范圍[J].系統工程理論與實踐,2000(5):121-124.
[9] 何慶飛,陳桂明,陳小虎,等.基于改進灰色神經網絡的液壓泵壽命預測[J].中國機械工程,2013,24(4):500-506.
[10] 王志平.基于指標體系的網絡安全態勢評估研究[D].長沙:國防科學技術大學,2010.

