摘  要： 傳統的OD矩陣估計方法大部分都是基于路段流量的，由于路段流量數目遠小于OD對的個數，因而限制了這些方法的推算精度。針對擁堵路網，提出了一種基于路段轉向流量的OD估計方法，以提高OD估計的精度。分析了路段轉向流量能夠降低OD的可行解集的范圍。通過雙層規劃模型求解擁擠路網上OD估計問題。由于最大熵模型不依賴于先驗OD矩陣，可以應用到更多的OD估計場景中，因此上層模型采用的是最大熵模型，下層采用用戶均衡模型。實驗結果表明：基于路段轉向流量可以增加估計的精度。

　　關鍵詞： OD矩陣估計；路段轉向流量；最大熵模型；用戶均衡模型；雙層規劃模型

0 引言

　　OD矩陣（Origin-Destination matrix），描述了一段時間內交通網絡的所有起點到終點的交通出行量，反映了交通出行者對交通網絡的基本需求。OD矩陣是城市交通規劃、控制、交通流預測和智能交通系統[1]等的重要基礎數據。而獲取OD矩陣的傳統方法需要非常大的時間成本和經濟成本。一種替代的方法就是通過更易獲取的路段流量和相關信息等來估計OD矩陣。

　　近幾十年，已經有許多模型被開發出來用于OD估計，如最大熵模型[2]、廣義最小二乘模型[3]、貝葉斯統計推斷模型[4]和極大似然模型[5]等。上述的幾種模型都將交通分配矩陣作為常量處理，即交通出行者的路徑選擇行為與OD矩陣無關，這種方法只適合擁擠效應不明顯的路網，一般是交通量較小的路網。而在實際情況中，許多路網都是擁擠路網。擁擠路網的交通分配模型更加接近于用戶均衡模型（UE）[6]，交通出行者的路徑選擇受OD矩陣的影響，即不同的OD矩陣會產生不同的交通分配矩陣。YANG H提出了將OD估計和交通分配過程進行綜合考慮的雙層規劃模型[7]。在雙層規劃模型中，交通分配矩陣由模型本身確定，不是給定的常量，非常適合擁擠路網的OD估計問題。以上方法均是基于路段流量，通常情況下，由于路段流量的個數遠小于OD對個數，OD矩陣可行解集較大，限制了OD估計的精度。于凱在最大熵模型中引入路段轉向流量[8]，增加了模型的估計精度，但是模型基于不變的分配矩陣，不適用于擁擠網絡。

　　近年來，一些新的觀測手段用于OD估計，比如手機信息、GPS信息，這些信息可以增加OD估計的精度，但是不易獲取而限制了其應用。通過傳統方法進行OD估計仍然為目前的主要方法，本文基于易于獲得的路段轉向流量，提出了一種基于路段轉向流量的OD估計雙層規劃模型。仿真實驗表明：該方法可以提高擁擠路網OD估計的精度。

1 基于路段轉向流量的OD估計模型

　　1.1 OD估計基本原理

　　交通網絡可以用一個有向圖G（V，E）表示，V為所有路段的集合，E為所有節點的集合。假設交通網絡有m個路段觀測流量，n個待估計的OD對，則基于路段流量的OD估計的基本方程組如下：

　　r=pq（1）

　　r=[r1r2…ri…rm]T，為路段觀測流量向量；

　　q=[q1q2…qi…qn]T，是待估計的OD矩陣的向量形式；

　　p是m×n的交通分配矩陣，描述了路段流量r和OD向量q的線性關系；

　　p=[p1Tp2T…piT…pmT]T，其中（pi）1×n表示了第i個路段流量ri與q的線性關系。

　　OD估計問題就是在已知r和p的情況下求解方程組（1）的解q，通常情況下由于m<<n，q有無窮多解。為了求得唯一的q，可以引入一些模型將OD估計變為一個數學規劃問題，形式如下：

　　min f（r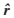，，q0，q）

　　s.t. r=pq（2）

　　q≥0

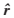　　：OD估計時求得的路段流量；

　　q0：先驗OD矩陣。

　　1.2 引入路段轉向流量的基本方程組

　　設第i個路段有si個轉向，ri1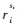，…，分別表示第1個，…，第si個轉向流量。根據路段流量守恒有：

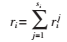　　（3）

　　第i個路段的第j個轉向流量方程可以表示為：

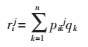　　（4）

　　pikj表示第k個OD量qk分配到i個路段的第j個轉向流量rij的比例。

　　由式（4）易知同一個路段的流量方程與路段轉向流量方程組線性相關，因此可以用路段i的轉向流量方程組代替關于路段流量ri的方程，則可將式（1）的方程組改為：

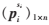　　表示了路段轉向流量與q的線性關系。上面的方程組也可以表示為：

　　rl=plq（6）

　　rl表示既有路段流量，也有轉向流量的向量；

　　pl矩陣表示rl與OD向量q的線性關系。

　　同理，其他有轉向流量的路段都能引入到方程組r=pq中。實際上，一個路網的許多路段都能引入幾個轉向流量，使得方程組的個數增加，結果就是矩陣pl的秩增加，q解集的范圍降低。

　　1.3 雙層規劃模型

　　雙層規劃模型的上層模型是最大熵模型EM，表示如下：

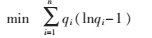
　　s.t. r=pq（7）

　　q≥0

　　已知r和p，模型EM可求得OD向量q。

　　分配矩陣p可以由下層模型（UE模型）解得。

　　其中，δis為1表示路徑s經過路段i，否則為0；fi表示路徑流量；W表示所有的路徑集合；Wi表示OD對i之間的所有路徑集合；ce（x）是路段旅行費用函數。

　　已知q，UE模型可以求得估計流量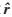，分配矩陣p。

　　引入部分路段上的轉向流量后可以將上層規劃模型EM中的等式約束改為rl=plq。

　　下層UE模型也可以求得估計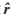，分配矩陣pl。

　　將基于路段流量的模型簡述為BEMR，基于路段轉向流量和路段流量的模型簡述為BEML。

2 求解算法步驟

　　由于雙層規劃問題本身有非凸、非光滑的特性，求取最優解非常困難，大部分算法只能針對特定的模型給出近似解。本文給出的迭代求解方法可以求得近似較優解。單獨求解上層最大熵問題（EM）和下層用戶均衡分配問題（UE），目前都有比較有效的算法。并且引入了路段轉向流量后，上層問題的搜索的可行解集的范圍大大縮小，也使得求解這個雙層規劃問題的一個相對較優的解更加容易。

　　求解這類雙層規劃問題的有效算法是迭代優化算法。算法的主要思想就是先給出上層規劃的初始決策變量，將這個決策變量傳遞到下層規劃中，下層規劃求解最優解，再將下層規劃的最優決策傳遞到上層規劃進行求解，如此反復求解上層規劃和下層規劃，最后雙層規劃問題的上層決策變量和下層決策變量趨于平穩，此時就是雙層規劃問題的相對較優的方案。根據這個方法，求解最大熵雙層規劃模型的思想是，先設定一個初始的OD矩陣求解下層的用戶均衡交通分配問題，將下層規劃求得的交通分配矩陣傳遞到上層最大熵模型中，并求解出最優的OD矩陣，最后模型趨于平穩，求得較優解。

　　用Q表示OD總量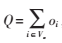，，Vo表示所有入口節點集合，oi表示O點的流量，通常情況oi都是很容易觀測到的，所以可以將Q作為一個常量處理。因為沒有先驗OD矩陣，而通過分析入口處交通總量來獲取初始迭代點是非常簡單可行的，所以可以用交通總量的平均值作為初始點。

　　求解步驟如下：

　　（1）初始化qk=[q1k…qik…qnk]T，k=0，其中每個qik=Q/n。

　　（2）用qk求解下層規劃問題，本文采用Frank-Wolfe算法求解，在這一步可以求得plk。

　　（3）用rl和plk求解上層規劃問題來獲取qk+1。設plk、rl分別是t×n的矩陣，t×1的向量（t>m），解決此問題，先引入拉格朗日乘數向量（λk）t×1，OD矩陣可以用拉格朗日乘數表示如下：

　　求解λk，將qk+1代入到（6）中有：

　　本文用Levenberg-Marquardt算法求解上述非線性方程組。求得λk，由式（9）就可以求得qk+1。

　　（4）檢查終止準則，若不能終止則轉步驟（2），并令k=k+1。終止準則由下式決定：

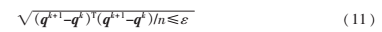
　　其中，ε為誤差上限值。

3 仿真實驗與分析

　　一個六路口的實驗網絡如圖1所示，一共34個路段，90個OD對。除了10個出口路段，其他路段均有3個轉向流量。基于路段流量的方程組總數為34個，基于路段流量和路段轉向流量的方程組總數為24×3+10=82個，其中有部分方程是線性相關的。

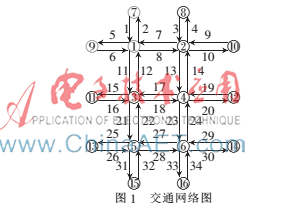
　　仿真實驗中用一個真實的OD矩陣按照用戶均衡模型分配到路網上，將分配所得的路段流量和路段轉向流量作為OD估計的輸入數據。根據估計所得的OD矩陣和真實的OD矩陣，比較BEMR模型和BEML模型的OD估計精度。

　　路段旅行費用函數采用BPR公式（Bureau of Public Road）：

　　ce（re）=ce（0）（1+0.15（re/Ce）4）（12）

　　Ce為道路通行能力；

　　ce（0）為平均自由流下的道路通行時間。

　　下面的統計參數可以表示OD估計的精度：均方根誤差rmse，相對均方根誤差trmse，相對平均值誤差mae。

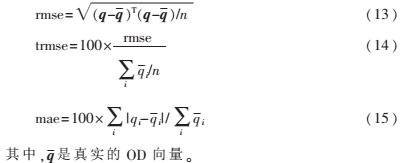
　　除此之外，還給出一個直觀的指標?茲x，表示OD估計的結果中與真實OD相對誤差小于等于x的OD對個數占總OD對個數的百分比。表示如下：

　　其中，card表示取集合元素總數。

　　表1為模型估計精度對比。從表1可以看出，基于路段流量和轉向流量的模型各項統計指標均優于單純基于路段流量的模型。當路網的路段流量和路段轉向流量均可觀測時，路段流量總約束條件為34個，而路段流量和轉向流量的總約束條件為82個，顯然后者包含的信息量更多，這使得OD估計的精度提高。

4 結論

　　采用基于轉向流量的OD估計算法，能有效降低數學規劃問題的可行解集的范圍，提高了解的準確性。隨著檢測技術的進步，越來越多的城市能提供準確的轉彎流量數據。實驗結果表明：基于路段轉向流量的OD估計的估計精度優于傳統的基于路段的OD估計。

參考文獻

　　[1] 丁革媛，李振江，鄭宏云.智慧城市中的智能交通系統構建[J].微型機與應用，2013，32（24）：1-3.

　　[2] VAN ZUYLEN H J， WILLUMSEN L G. The most likely trip matrix estimated from traffic counts[J]. Transportation Research Part B： Methodological， 1980，14（3）：281-293.

　　[3] CASCETTA E. Estimation of trip matrices from traffic counts and survey data： a generalized least squares estimator[J]. Transportation Research Part B： Methodological， 1984，18（4）：289-299.

　　[4] MAHER N J. Inferences on trip matrices from observations on link volumes： a Bayesian statistical approach[J]. Transpor-tation Research Part B， 1983，17（6），435-447.

　　[5] SPIESSH. A maximum likelihood model for estimating origin-destination matrices[J]. Transportation Research Part B： Methodological， 1987，21（5）：395-412.

　　[6] SHEFFI Y. Urban transportation networks： equilibrium analysis with mathematical programming methods[M]. Englewood Ciiffs： Prentice-Hall Inc， 1985.

　　[7] YANG H， SASAKI T， IIDA Y， et al. Estimation of origin-destination matrices from link traffic counts on congested networks[J]. Transportation Research Part B， 1992， 26（6）， 417–434.

　　[8] 于凱.基于轉彎流量的OD反推算法及基于微觀對象的動態配流算法研究[D].杭州：浙江大學工業控制技術研究所，2006.