摘 要: 能譜平滑是能譜分析過程中必不可少的環節,對消除數據的統計漲落以減少后續分析誤差有著重要的意義。圍繞能譜平滑的典型頻域平滑算法,即離散傅里葉變換(DFT)平滑法,在LabVIEW平臺下對其進行了仿真實現,并討論了平滑參數對平滑輸出的影響。運行結果表明,截斷頻率取值越低,降噪后能譜光滑效果越好,截斷頻率取值越高,光滑作用減弱,但降噪后的譜形與原始譜形越接近。在實際應用中,通過調整該平滑參數,能夠使能譜取得理想的平滑效果。
關鍵詞: 能譜平滑;離散傅里葉變換;LabVIEW
0 引言
不同核素放射出具有不同能量的射線,因此顯現的能譜也不同。能譜橫軸為道址,道址越高,其表征的能量越高;縱軸為計數值,計數與射線強度呈正比。對能譜的處理和分析可用于判定核素的種類及含量。由于電子系統本身存在的噪聲影響,能譜數據會有比較大的統計漲落,進而導致數據處理的誤差。因此,譜數據處理與分析的首要步驟就是譜平滑,利用該方法來減少統計漲落對分析結果產生的負面影響[1]。本文利用LabVIEW在支持用戶計算機仿真、數據處理與分析、人機交互等方面的優勢,設計了離散傅里葉變換平滑法的譜平滑器,在實現能譜的平滑功能的同時,為譜數據處理與分析的軟件設計提供了參考。
1 離散傅里葉變換平滑算法原理
多道譜數據的平滑,從實現本質上都可視為數字濾波的范疇,要求平滑后的數據應盡可能保留平滑前數據中有意義的特征,尤其是峰的形狀和面積不能產生很大的變化[2]。常用的平滑方法總體上可歸為時域法或頻域法,而傅里葉變換法是一種最典型的頻域譜平滑法[3]。
傅里葉變換的實質是將信號表示為各個頻率諧波函數分量的疊加,對信號函數的研究可轉變為對疊加權系數的研究。該方法作為一種頻域平滑法,其基本思想是通過傅里葉變換后的信息抑制高頻系數,即濾去高頻噪聲,進而達到譜圖平滑效果[4]。對于連續函數的傅里葉變換如式(1)所示。

由于譜數據的道數為整數值,譜線以對應的離散化數據序列出現,需對連續傅里葉變換進行離散變形。在時間、頻率都不連續的情況下,離散傅里葉變換式(DFT)及逆變換式(IDFT)分別如式(2)和式(3)所示。
![W()YS8FT)%$$(A]$~L%7{T3.png W()YS8FT)%$$(A]$~L%7{T3.png](http://files.chinaaet.com/images/2016/02/22/6359174631175100009739190.png)
在式(2)和式(3)中,m為DFT輸出序列號(m=0~N-1),n為輸入的時間信號序列號,N為輸入(輸出)序列總數。對能譜平滑的具體步驟為:(1)將原始能譜數據進行逐一DFT,獲取其頻譜序列(輸出具有對稱性),其分解頻率為其分解頻率為fa(m)=mfs/N(fs為采樣頻率);(2)根據得到的頻譜對不需要的頻率量抑制;(3)對頻譜做IDFT,得到平滑后的能譜[5]。
2 仿真實現與分析
2.1 前面板設計

平滑器的設計包括前面板與程序框圖兩個部分的設計[6]。前面板運行效果如圖1所示。波形圖控件用于顯示讀取的能譜數據以及經快速傅里葉變換(FFT,離散傅里葉變換的一種快速算法)后的能譜信號頻譜。輸入控件供用戶根據信號頻譜輸入截斷頻率,為平滑提供參數。此外,面板還包括顯示格式、平滑狀態、文件數據信息。
2.2 程序框圖設計
按下“讀取數據”、“平滑”、“停止”按鈕可激活相應的事件。“讀取數據”的響應為打開格式是二進制的譜數據文件,計算能譜信號頻譜并送顯示控件[7]。“平滑”的響應為按照截斷頻率對信號頻譜進行抑制,再對頻譜作快速傅里葉逆變換(IFFT)得到平滑后的譜數據送顯[8]。平滑算法的程序實現如圖2所示。

2.3 運行結果及分析

讀取的譜數據樣本以及進行離散傅里葉變換后的頻譜序列(序列總數為1 024,采樣頻率默認為1 000)如圖3、圖4所示,由于頻譜序列具有對稱性,因此圖上給出了完整頻譜圖的左半部分。由圖可知,能譜數據噪聲集中在高頻部分,因此從理論上對能譜進行低通濾波便可達到平滑效果。
根據離散傅里葉變換平滑法的原理,低通濾波后的效果與選取的截斷頻率有關。由頻譜圖可知,當頻率大于20 Hz后能量迅速衰減,大于100 Hz后其頻譜分量幾乎為零。分別選取截止頻率為75 Hz、150 Hz、250 Hz,對大于截止頻率的頻段進行抑制,再進行離散傅里葉反變換后得到的平滑效果如圖5所示。從總體效果來看,離散傅里葉變換平滑法通過高頻抑制能夠對能譜起到平滑作用[9]。
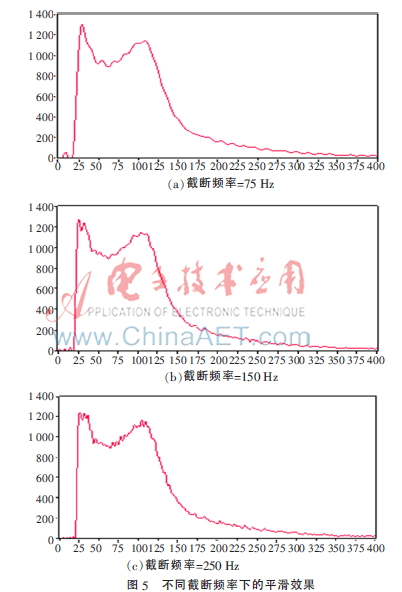
從不同截斷頻率下的平滑降噪效果來看,截斷頻率取得越小,其光滑效果越好,但與原始譜的差異也就越大,在消除噪聲的同時過濾掉了一些有用的高頻信息;截斷頻率取得越大,光滑能力也越弱,其平滑后的譜形與原譜保持的相似性越強;截斷頻率取得過大則可能導致平滑失效。由此,在實際應用時應該針對不同特征的譜數據選取合適的截斷頻率,例如對于統計漲落很大且峰形單一清晰的能譜,截斷頻率可取得稍小一些;對于形狀復雜、弱峰較多的能譜宜將截斷頻率取得大一些,以降低原始能譜形狀在平滑后發生畸變的可能性。
3 結論
通過對平滑器的仿真實驗,離散傅里葉變換法能夠起到能譜平滑作用。由于平滑前需要知道截止頻率,采用人工判斷的方式不利于平滑功能的快速實現,因此后續可在自動判別能譜平滑參數方面對平滑器進行優化。同時,基于LabVIEW在圖形化編程方面的簡單、直觀與高效性[9],在能譜平滑器中可適當添加平滑算法,根據不同特征的能譜擇優選取平滑方法,以達到最佳的平滑效果。
參考文獻
[1] 夏文明,賈銘椿,郭智榮.基于LabVIEW的γ能譜降噪處理[J].核電子學與探測技術,2009,29(5):959-961.
[2] 覃章健.基于FPGA的便攜式數字核譜儀研制[D].成都:成都理工大學,2008.
[3] Argonne National Laboratory. Report of workshop on digial electronics for nuclear structure physics[R]. 2001.
[4] 袁新宇,劉良軍,周劍良.γ能譜濾波方法比對研究[J].南華大學學報(自然科學版),2011,25(2):1-5.
[5] 史東生,弟宇鳴,周春林.小波變換與傅里葉變換在γ能譜降噪處理中的比較研究[J].核電子學與探測技術,2006,26(6):134-137.
[6] 吳成東,孫秋野,盛科.LabVIEW虛擬儀器程序設計及應用[M].北京:人民郵電出版社,2008.
[7] 王亞凡,張秉仁,閆立東.基于LabVIEW的多功能虛擬頻譜儀的設計[J].電子技術應用,2014,40(12):101-103.
[8] 陳樹學,劉萱.LabVIEW寶典[M].北京:電子工業出版社,2013.
[9] 藍賢桂.γ能譜儀的初步研發及基于Labview的譜處理技術[D].撫州:東華理工大學,2012.

