文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2016.12.004
中文引用格式: 王丹丹,王軍,王林. 納米級MOSFET亞閾值區電流特性模型[J].電子技術應用,2016,42(12):19-22,26.
英文引用格式: Wang Dandan,Wang Jun,Wang Lin. A model of subthreshold current characteristics for the nanoscale MOSFET[J].Application of Electronic Technique,2016,42(12):19-22,26.
0 引言
集成電路對高集成度、低功耗和工作頻率的需求不斷提高,使得CMOS技術不斷發展。但對于產品設計來說,漏極電流和柵極電流作為MOS器件的重要直流參數,是器件建模和仿真的難點和核心,同時能夠準確預測MOSFET高頻電流特性的物理數學模型也是至關重要的[1]。
目前對圍繞納米級MOSFET的性能提升、物理模型的研究已成為國內外研究的熱點,其中電流特性模型是MOSFET器件和電路進行直流分析、交流小信號分析、噪聲分析等的重要基礎[2]。然而文獻報道中的器件特性模型,主要聚焦于MOSFET強反區直流漏極電流、電導、本征電荷和本征電容的研究上[3],對于亞閾值區漏電流和柵極電流的研究卻鮮有報道。文獻[4]提出了傳統的長溝道漏電流模型,揭示了強反區漏電流平方律特性,卻缺乏亞閾值區的研究。文獻[5-7]闡述了傳統長溝道MOSFET柵極電流模型推導,但隨著器件進入納米級,工作頻率升至吉赫茲以上,已不能準確描述出現的所有新特性,且描述出的電學特性之間總有不自洽存在。
基于器件亞閾值區,本文建立了納米級MOSFET漏電流模型和柵極電流模型,同時加強了器件電流的頻率與偏置依賴性建模來反映器件電流特性。對于亞閾值區電流模型,基于亞閾值區反型電荷,而不是采用傳統的有效溝道厚度近似的概念,從而提高了模型的精確度。同時將所建模型的仿真結果與實驗測量結果進行了比較,驗證了模型的準確性。該模型的建立為納米級MOSFET的分析和設計提供了參考,推導出的I/V特性方程更容易將抽象級別從器件物理級別提升到電路級。
1 電流模型
圖1是納米級NMOSFET結構示意圖,其中采用了電荷模型。漏極電流和柵極電流特性模型是納米級NMOSFET器件和電路進行直流分析、交流小信號分析、噪聲分析等的重要基礎,因此對分析研究納米級NMOSFET器件的電流特性很有必要。

1.1 漏極電流
基于器件中載流子的隨機運動,運用擴散漂移理論,納米級MOSFET器件中漏極電流可表示為:

其中αn為碰撞電離率,QI(x)為器件單位面積反型層電荷數,V(x)為加在x點上的電壓,Vth為熱電壓,W為溝道寬度,un為載流子遷移率,Dn為擴散系數,Dn=unkT/q。當器件工作強反區時(柵壓大于閾值電壓,Vgs>VT),相對于器件溝道中漂移電流來說,此時可以忽略擴散電流,總電流中漂移電流為主導,即Ids=Ids1。然而隨著Vgs的不斷減小,漏電流也不斷降低,當Vgs接近VT或者小于VT時,納米級MOSFET器件的I/V特性從平方律變為指數律,而此時的電流稱之為亞閾值電流。當器件工作在亞閾值區,勢壘表面的可動載流子遷移率較低,溝道電流以擴散電流為主[8],即:

當器件工作在亞閾值區,反型層電荷濃度和耗盡層電荷濃度相比可以忽略不計,從源端到漏端的表面勢可視為常數[9-10],通過求解泊松方程可得到表面勢表達式為:
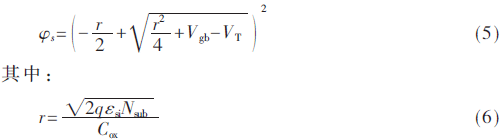
式中,εsi為硅的介電常數,Nsub為襯底的摻雜濃度,Cox是柵氧電容。由表面勢可進一步求得溝道反型層單位面積電荷數為:
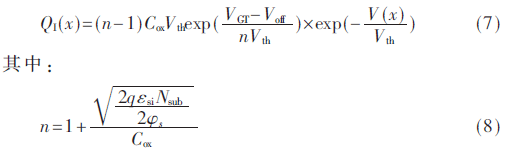
式中,VGT=Vgs-VT為柵極過載,Voff為補償電壓。
由上式可以推導納米級MOSFET亞閾值區漏電流為:
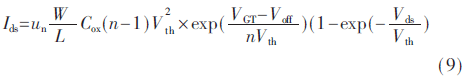
1.2 柵極電流
感應柵極電流是由溝道內的波動電勢通過柵極電容的耦合效應,引起了柵極極板的噪聲電流。如圖1所示,柵極感應噪聲電流可以表示為[11]:

2 結果及分析
為驗證本文所建立的納米級MOSFET亞閾值區漏電流模型和柵感應電流模型的準確性,首先將擬合參數代入模型后,利用MATLAB進行仿真,然后將仿真結果與實驗測量結果相比較來驗證模型的準確性,同時分析不同偏置條件下的器件電流特性。
圖2所示為亞閾值區納米級MOSFET的輸出特性曲線。從圖中可以看出,曲線1、曲線2和曲線3分別是柵極偏置為Vgs=0.15 V,Vgs=0.2 V和Vgs=0.25 V時的輸出特性曲線。當Vds很小時,漏電流Ids將隨著Vds上升而迅速增大,輸出特性曲線的斜率較大。在一定柵極偏置條件下隨著Vds不斷增加,漏電流開始飽和,是由于亞閾值區溝道反型層存在載流子濃度梯度,靠近源端高,靠近漏端低,電流以擴散電流為主。
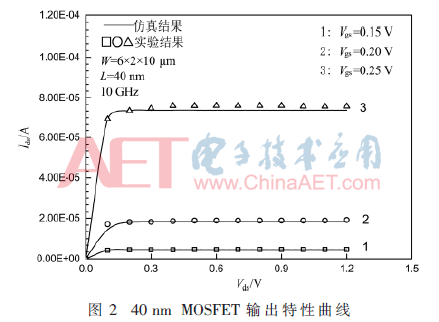
圖3為亞閾值區MOSFET轉移特性曲線,圖3(a)為線性坐標,圖3(b)為半對數坐標。從圖中130 nm和40 nm MOSFET漏電流對比分析可以看出,在亞閾值區,漏電流很小且隨著Vgs的減小,其值以指數形式急劇下降,是由于在亞閾值區漏電流以擴散電流為主導,由源漏兩端的電荷濃度差決定,而亞閾值區源端電荷濃度和Vgs呈指數關系,因此漏電流和Vgs呈現指數關系,具有很強的偏置依賴性。仿真結果與實驗結果的良好吻合,證明了該模型的準確性,同時也說明本文漏電流模型等比例縮小的可行性。

圖4為亞閾值區MOSFET柵感應電流隨柵極偏壓的變化曲線,圖4(a)為線性坐標,圖4(b)為半對數坐標。通過圖中130 nm和40 nm MOSFET漏電流對比分析可以看出,溝道越短,亞閾值區漏電流越大,Ig隨著Vgs的增大以指數形式增加。這是由于隨著溝道長度的減小,使得源漏極耗盡區在溝道中的比重增大,反型層所占比重減小,本征載流子濃度提高,溝道反型層電子密度提高;同時Vgs增大,導致氧化層電場增強,致使溝道表面電子的耦合效應以及碰撞頻率均增大。分析發現,柵感應電流與漏電流相比,Ig具有跟隨性。

圖5為亞閾值區電流隨頻率變化的關系,圖5(a)為漏電流隨頻率變化的關系,圖5(b)為柵感應電流隨頻率變化的關系。從圖中可以看出,一定偏置條件下漏電流具有頻率獨立性,而柵感應電流具有強烈的頻率依賴性,與頻率成線性比例。在亞閾值區,當頻率升高時,溝道縱方向上載流子的熱運動加劇,耦合效應和碰撞頻率就越明顯,感應柵極電流噪聲也就越高,而橫向方向上,主要由溝道電子面密度所決定。

3 結論
本文針對納米級MOSFET器件物理結構,運用漂移擴散原理分別建立了亞閾值區漏極電流模型和柵極電流模型。其中模型引入了頻率與偏置依賴性來反映器件電流特性,同時將所建模型的仿真結果與實驗測量結果相比較,驗證了模型準確性。并且對于亞閾值區電流模型,基于亞閾值區反型電荷,而不是采用傳統的有效溝道厚度近似的概念,從而提高了模型的精度。通過不同偏置條件下的對比分析表明亞閾值區漏極電流模型具有等比例縮小的可行性,柵極電流具有跟隨性和頻率依賴性。
參考文獻
[1] CHAUHAN Y S,VENUGOPALAN S,CHALKIADAKI M A,et al.BSIM6:Analog and RF compact model for bulk MOSFET[J].IEEE Transactions on Electron Devices,2014,61(2):234-244.
[2] PARVIZI M,ALLIDINA K,EL-GAMAL M N.A sub-mW,ultra-low-voltage,wideband low-noise amplifier design technique[J].IEEE Transactions on Very Large Scale Integration Systems,2015,23(6):1111-1122.
[3] CHALKIADAKI M A,ENZ C C.RF small-signal and noise modeling including parameter extraction of nanoscale MOSFET from weak to strong inversion[J].IEEE Transactions on Microwave Theory & Techniques,2015,63(7):1-12.
[4] 拉扎維.模擬CMOS集成電路設計[M].西安:西安交通大學出版社,2003.
[5] ARORA N.Modeling hot-carrier effects[M].MOSFET Models for VLSI Circuit Simulation.Springer Vienna,1993:366-401.
[6] TRIANTIS D P,BIRBAS A N,PLEVRIDIS S E.Induced gate noise in MOSFETs revisited:The submicron case[J].Solid-State Electronics,2010,41(12):1937-1942.
[7] CHAN L H K,YEO K S,CHEW K W J,et al.High-frequency noise modeling of MOSFETs for ultra low-voltage RF applications[J].IEEE Transactions on Microwave Theory & Techniques,2015,63(1):141-154.
[8] ARORA N.Mosfet modeling for vlsi simulation:theory and practice(International series on advances in solid state electronics)[M].World Scientific Publishing Co.Inc.2007.
[9] TSIVIDIS Y.Operation and modeling of the MOS transistor[M].McGraw-Hill,Inc.1999:25-39.
[10] 呂懿,張鶴鳴,胡輝勇,等.單軸應變Si n型金屬氧化物半導體場效應晶體管源漏電流特性模型[J].物理學報,2015(19):272-277.
[11] VAN L R,PAASSCHENS J C J,SCHOLTEN A J,et al.New compact model for induced gate current noise[C].Electron Devices Meeting,2003.IEDM′03 Technical Digest.IEEE International.IEEE,2003:36.2.1-36.2.4.

