高揚1，滕奇志1，熊淑華1，何海波2

　　（1.四川大學 電子信息學院圖像信息研究所，四川 成都 610065；2.成都西圖科技有限公司，四川 成都 610065）

       摘要：巖心CT圖像中相鄰顆粒之間存在相互粘連，粒度參數分析等需要對粘連顆粒進行分割。結合巖心粘連顆粒的特性，提出一種基于模糊距離變換的改進顆粒分割算法。首先，對預處理后的巖心圖像進行模糊距離變換并提取出距離信息的灰度圖像，然后利用形態學膨脹重構方法提取標記作為后續分水嶺算法的種子點，根據種子點采用一種基于測地重建的改進分水嶺算法得到相鄰種子點之間的分割線，最后完成粘連顆粒的分割。實驗結果表明本文算法可以提高粘連顆粒分割的準確度并減輕分水嶺算法的過分割現象。

　　關鍵詞：巖石顆粒；模糊距離變換；分水嶺；

　　中圖分類號：TP391文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.04.014

　　引用格式：高揚，滕奇志，熊淑華，等.基于模糊距離變換的巖心圖像顆粒分割算法［J］.微型機與應用，2017,36（4）：47-50.

0引言

　　隨著計算機斷層掃描（CT）技術的日漸成熟與普及，石油地質行業也開始使用該技術分析巖石的結構特性。巖心CT圖像中粘連的巖心顆粒會影響粒度等參數分析。通常CT圖像是一個二維灰度圖像序列，因此可以先對二維圖像進行粘連顆粒分割，通過二維分割降低三維重建后三維顆粒的分割難度。

　　圖像分割［12］是為了更好地將具有類似特征性質的元素歸在同一個集合中，它也是圖像處理與后續分析識別的關鍵步驟。近年來不少學者在粘連圖像分割方面做了大量相關的工作，提出了基于圖論［3］、形態學［4］、邊緣檢測、區域分割、Snake模型、神經網絡等多種分割算法。而這些算法都有各自具體的應用場合與約束限制。

　　分水嶺算法［5］作為一種經典的圖像分割算法，有許多在此基礎上的改進與拓展算法。例如基于距離變換的分水嶺算法［6］、多分辨率分水嶺算法、梯度修正與區域合并分水嶺算法［7］、基于蟻群的分水嶺算法等。由于傳統分水嶺算法有過分割且耗時較長等缺點，文獻［8］提出了一種改進的分水嶺分割算法，文獻［9］在文獻［8］的基礎上利用改進的形態學重構方法刪除、合并了部分種子點，濾除了部分錯誤的距離變換信息并利用近似歐式模板計算顯著降低了算法的時間復雜度，使用測地重建的方式改進分水嶺算法并得到了較為正確的分割效果。但該算法仍存在局部過分割和種子點提取不恰當及后續分割線劃分不準確的現象。

　　本文在文獻［9］的基礎上提出了一種基于模糊距離變換及生長速率控制的改進分割算法。該算法提升計算距離變換準確度，并使形態學重建之后得到的種子點形態更接近待分割顆粒，繼而使隨后進行的區域生長得到更準確的分割線。并且在分割過程中依據種子點的等效圓直徑控制區域生長速度以使分割更加準確合理。

1模糊距離變換及區域生長控制

　　文獻［9］中基于二值圖的近似歐式距離變換會造成最終得到的種子點幾何形態與待分割顆粒的形態相似度不高。而在后續進行測地重建分割算法中，利用種子點進行區域生長后的種子點形態與實際顆粒區別較為明顯，從而也使分割線的形狀與位置出現明顯的偏差。圖1(a)是尺寸為199×197的大顆粒巖心圖像，經過距離變換后的結果圖如圖1(b) 所示，其中灰白色部分為種子點。

　　標記種子點與待分割顆粒形狀吻合度不高，會導致后續測地重建算法得到的分割線存在偏移。

　　針對圖1中發現的缺點，本文對該問題進行了改進。利用模糊集在距離變換中的應用改進了尋找種子點的方法，使其更加貼近于待分割顆粒形態，并有效減少了種子點提取數量的規模，從一定程度上減輕了過分割現象。

　　1.1模糊子集與模糊距離

　　ZADEH L A在1965年提出了模糊集［10］的概念，在這個集合中兩點之間的最短距離再也不是一條簡單的直線。設X為參考集，它的模糊子集A定義為：

　　A={(x,μA(x)|x∈X)},μA(x):X→［0，1］(1)

　　其中μA(x):X→［0，1］為A的隸屬度函數。本文根據巖心圖片無規則特性選擇的隸屬度函數為高斯函數，公式如下：

　　其中f(p)為圖像灰度函數，mA為灰度的平均值，σA為灰度的標準差，GmA,σA為未規范化的高斯函數。

　　圖2最短路徑示意圖在模糊集中的兩點最短路徑不一定是一條直線。圖2為兩種不同灰度集組成的圖像，顯然像素點p、q的最短路徑不是經過灰色區域的直線而是由淺灰色區域的元素組成的線段如路徑L。

　　假設I（p,q）表示p到q之間所有路徑的集合。對于任意的一條路徑π∈I(p,q)，有π=<p=p1,p2,p3,pn,pm=q>，其中pi∈π,1≤i≤m。那么設相鄰兩點k,n之間的模糊集距離<k,n>定義為：

　　<k,n>=12(μ(k)+μ(n))≤k-n(3)

　　對路徑π記η為路徑的總長度，計算公式可以定義為：

　　其中，μ(pi)表示點pi對于某個模糊集的隸屬度，pi-pi+1表示i、i+1兩點間的歐式距離。

　　模糊距離是在模糊集上的所有有效路徑長度中的最短路徑長度，其中路徑π∈I(p,q)的最小值為（p,q）=min{η(π)}。而對于單獨的一個目標點p，用ω(p)表示p到最近背景點的距離，表達式為：

　　ω(p)=min{(p,q)}(5)

　　那么便可以得到對應點的模糊集隸屬度為：

　　

　　根據上述原理可以將模糊集理論與距離變化結合應用于種子點的提取，具體步驟如下。

　　(1）對目標與周圍背景使用模板計算灰度值的期望和方差統計信息，使用模糊集變換公式生成每點對應的高斯隸屬度信息；

　　(2）在計算目標到背景距離變換時加入高斯隸屬度權重約束，最終得到與目標形態相關的距離值。

　　通過這個算法在尋找種子點過程中提供當前像素點的隸屬度，反映該像素點與背景像素在幾何形態上的關系。為了更好地獲取準確種子點，同時對種子點進行腐蝕膨脹、濾波等一系列的形態學處理。最終獲取更加準確的種子點形態，為后續分割提供了較好的區域生長形態基礎。

　　1.2區域生長速率控制

　　測地重建算法就是以種子點為中心進行不同區域劃分的局部生長算法。對每個種子點使用該算法就能得到所有分割線的數組集合。傳統分水嶺區域生長算法默認種子點使用固定的增長速度。而在相鄰顆粒形態差別較大的情況下，固定閾值生長得到的分割線會出現較大誤差。

　　由于得到的種子點形態大小不一致，本文采用每個種子點的等效圓直徑來控制各自區域增長速度，以得到較為準確的分割線集合。其中種子點的生長速率為：

　　v=k*(sprt(S/π))(7)

　　其中k為常系數，S為種子點面積。

　　對圖1(a)巖心圖像使用傳統固定的生長速度得到的分割線以及采用生長速率控制獲得的分割線結果如圖3所示。

　　從圖3中明顯能看出，(a)中分割線向右偏移，而(b)中利用種子點進行速率控制后分割線更接近合理分割位置，也就使顆粒分割更加準確。

　　本文改進算法提取的種子點幾何形態接近顆粒形態，有利于得到更準確的分割線，并最終減輕分水嶺算法以及圖像噪聲干擾帶來的種子點過多的現象。同時采用控制區域生長速度的方法，使得到的分割結果更符合人類視覺特點。

2實驗結果與分析

　　首先將本文算法與文獻［7］中的改進算法應用到同一塊巖心的粘連顆粒CT序列圖中，用來對比說明在帶權隸屬度的約束下種子點提取會更加準確合理，同時會合并部分相鄰種子點減弱后續顆粒的過分割。在得到分割使用的種子點的基礎上，通過進一步對比分析同一樣本最終分割的結果，說明區域生長速率控制也會進一步提高分割的準確度。

　　2.1種子點提取結果對比

　　首先，比較分析本文算法與文獻［7］在提取種子點形態的差異以及種子點規模上的差距。分割選取了兩組不同特征的真實巖心樣本序列圖像進行分析，結果如圖4和圖5所示。其中圖4（a）的圖像是尺寸為347×357的巖心顆粒圖像1，圖像(b)、(c)分別為本文算法和文獻［7］算法提取顆粒的種子點疊加圖。圖5(a)為巖心顆粒圖像2，對應于圖1（a），對其分別使用本文算法和文獻［7］算法，提取的顆粒種子點疊加圖為(b)、(c)。

　　原始巖心圖像1和2在不同閾值下提取種子點所用時間及提取種子點數如表1所示。

注：FD表示本文算法，WF表示文獻［10］算法

　　從這兩組圖像中可以得知本文算法提取的種子點相對文獻［10］提取的種子點，在形狀方面更加貼近實際粘連顆粒，有利于后續確定分割線，其位置更接近顆粒中心，種子點數目也進一步合理減少，從而會使運算時間進一步縮短。這些優點均有利于后續測地重建算法尋找更準確的分割線段。

　　2.2分割結果對比

　　在上述兩組圖像提取了種子點的基礎上進行相應的測地重建并得到最終分割結果。對圖4(a)和圖5(a)分別使用本文算法與文獻［10］算法，分別得到如圖6(a)、(b)和圖7(a)、(b)兩組分割結果圖。

　　從圖6、圖7兩組分割結果中可以得到：顆粒的過分割和誤分割現象得到較為明顯的抑制，分割線的準確度也進一步提升。

　　圖6(a)、(b) 在不同分割閾值下的分割結果如表2所示。表2中本文算法分割線的減少也就意味著過分割和誤分割的幾率有所下降。

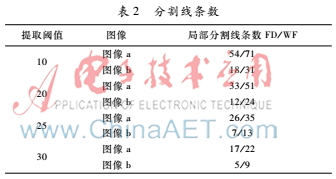
　　從上圖分析結果可以獲得以下結論：由于本文算法種子點提取區域位置更接近分割顆粒的中心，種子點幾何形態更加貼近分割顆粒的幾何形態從而使區域生長得到的分割線更加準確。同時通過本文算法分割結果與文獻［7］分割結果相比較可以看出，由于本文的距離變換使用了帶權的隸屬度約束種子點提取的個數，對最終顆粒過分割的抑制能力優于文獻［7］。生長速率控制也會使顆粒劃分的分割線更為準確。

3結論

　　為了較好地分割粘連巖心顆粒圖像，針對巖心圖像的特性，本文采用了一種基于模糊距離變換的改進分水嶺算法。在得到距離變換的圖像基礎上加入高斯隸屬度權值作為計算約束，然后優化距離模板計算并對種子點進行濾除、合并等操作，使后續區域生長效果更加良好。同時區域生長過程中控制不同大小種子點的生長速度以得到更為準確的分割線。實驗結果表明，本文的分割方法能較好地適合人眼視覺鑒定出粘連物體的分割線。參考文獻

　　［1］ 林開顏,吳軍輝,徐立鴻. 彩色圖像分割方法綜述［J］. 中國圖象圖形學報,2005，10（1）:1-10.

　　［2］ 羅希平,田捷,諸葛嬰,等. 圖像分割方法綜述［J］. 模式識別與人工智能,1999（3）:300-312.

　　［3］ BRYANT R E. Graphbased algorithms for Boolean function manipulation［J］. IEEE Transactions on Computers, 1986, 35(8):677-691.

　　［4］ 劉志敏, 楊杰. 數學形態學的圖象分割算法［J］. 計算機工程與科學, 1998, 20(4):2127.

　　［5］ 王國權, 周小紅, 蔚立磊. 基于分水嶺算法的圖像分割方法研究［J］. 計算機仿真, 2009, 26(5):255-258.

　　［6］ 侯慧, 石躍祥. 基于距離變換的改進分水嶺算法在白細胞圖像分割中的應用［J］. 計算技術與自動化, 2016, 35(3):81-84.

　　［7］ 盧中寧, 強贊霞. 基于梯度修正和區域合并的分水嶺分割算法［J］. 計算機工程與設計, 2009, 30(8):2075-2077.

　　［8］ 刁智華,趙春江,郭新宇,等. 分水嶺算法的改進方法研究［J］. 計算機工程,2010,36（17）:4-6.

　　［9］ 劉潔.巖心三維圖像顆粒分割相關技術研究［D］.成都:四川大學,2015.

　　［10］ ZADEH L A. Fuzzy sets［J］. Information & Control, 1965, 8(3):338-353.