文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.171176
中文引用格式: 張杰,王少超,關永. 基于形式化方法的有限域乘法器的建模與驗證[J].電子技術應用,2018,44(1):109-113.
英文引用格式: Zhang Jie,Wang Shaochao,Guan Yong. Modeling and verification of finite field multiplier using formal method[J]. Application of Electronic Technique,2018,44(1):109-113.
0 引言
有限域運算在代數編碼、數據加密和數字信息處理等領域有著廣泛的應用,其運算速度是加密算法運算速度的基礎[1];如今僅依靠軟件實現有限域乘法運算已經難以滿足人們對加密解密算法運算速度的需求,而已通過改用專門的硬件來滿足市場對有限域乘法運算速率的要求。但是,有限域乘法的硬件實現結構復雜,容易出現潛在的設計缺陷而導致運算錯誤,甚至會導致加密系統密鑰泄漏,從而給系統的信息安全帶來巨大威脅[2]。因此,對有限域乘法器的設計進行可靠性驗證是十分必要的。
眾所周知,常用的模擬和仿真驗證方法雖易于實現,但驗證過程中存在測試空間不完備的問題,難以排除所有的錯誤。而形式化方法則是使用形式語言分別對系統設計要求的功能和實現進行形式化描述,再通過基于相同形式語言的證明工具依據數學理論來驗證系統的正確性,它能保證所驗證性質的完備性。目前形式化方法主要有等價性驗證、模型檢驗、定理證明和計算機代數。等價性驗證和模型檢驗方法由于存在狀態空間爆炸問題,導致驗證的系統規模有限[3-4];計算機代數方法主要應用于數學證明,缺乏精確的邏輯概念,難以保障推導過程的可靠性[5-7];定理證明方法則需要對待驗證的系統實現和系統規范進行形式化建模,并在定理證明器中完成系統實現蘊含系統規范的證明,此法可有效地避免人為推演而造成的證明可靠性問題,更加有利于在驗證過程中快速找出驗證目標細微的缺陷和不足。
因此,本文選用基于高階邏輯的定理證明器HOL4系統作為驗證平臺,通過層次化方法和基于周期的方法對有限域乘法器形式化建模,并采用定理證明方法完成其可靠性的驗證工作。
1 有限域及域運算
1.1 有限域(finite field)
有限域是由一個有限元素的集合和兩個二元運算所組成,記為GF(p)[8]。有限域中的任意元素可以通過不同的基底來表示,本文以應用最廣、研究最多的多項式基有限域乘法器設計作為研究對象。
常見的有限域算術運算有加法、乘法、除法以及模逆運算等,本文工作僅涉及到加法和乘法,所以對其他有限域算術運算不做詳細說明。
1.2 有限域GF(2m)加法
有限域加法是通過標準的多項式加法運算來實現的,表達式如下:

1.3 有限域GF(2m)乘法
有限域乘法運算是加密算法和代數編碼的核心運算,基于多項式基的有限域乘法運算的通用表達式為:

由式(2)可知,基于多項式基有限域乘法運算分為兩個運行步驟:多項式乘法和多項式取模。傳統的有限域乘法依序執行多項式乘法和多項式取模運算,中間結果位數長,硬件實現資源消耗大,運算效率低。而基于最低位優先(LSB-First)的有限域乘法算法從乘數B的最低位開始通過交叉執行多項式乘法和多項式取模運算,可減少中間結果位長,縮短關鍵路徑,有效地降低乘法運算的空間復雜度和時間復雜度[9]。
所以,通過對式(2)進行一系列的變化可以得到基于最低位優先的有限域乘法的表達式,如式(3)、式(4)所示。

2 有限域乘法器的形式化建模
如前所述,基于定理證明方法對有限域乘法器進行形式化驗證,首先需要完成有限域乘法器的形式化模型,建模工作主要分為兩個部分:(1)依據算法特性抽取驗證的關鍵性質,即系統的規范,并基于高階邏輯完成相關性質的描述;(2)分析目標系統的實現電路,構建描述系統實現的高階邏輯表達式,即完成系統實現的形式化建模。
2.1 有限域乘法器規范的形式化建模
規范是敘述系統所需要具備的功能和性質。依據上述最低位優先算法,有限域乘法器的功能可描述為:乘法器對輸入的乘數InA、InB以及首一不可約多項式P(x)進行相應的多項式乘法和多項式取模運算,得到有限域乘法運算的最終結果C(x)。通過功能分析,可得到有限域乘法的兩個基本性質。
性質1:針對最低位優先算法中的式(3),當周期i=0時,則對A(x)i進行初始化置數操作,初始值為輸入的乘數InA,否則,A(x)i的取值等于上一迭代周期結果A(x)i-1左移一位后再對P(x)進行多項式取模,表述如下:
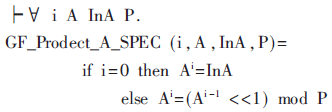
性質2:針對最低位優先算法中的式(4),當周期i=0時,則對部分積累加結果C(x)i進行初始置數操作,初始值為0;否則,式(3)中上一迭代周期得到的A(x)i-1和乘數InB的對應位bi的乘法運算結果,最后再和上一周期部分積結果C(x)進行累加得到當前周期的部分積累加值C(x)i,即:

由上文可知,對于有限域GF(2m),在最低位優先算法中需要通過m次循環操作才能獲得有限域乘法運算的最終結果,即C(x)=C(x)m。所以基于最低位優先的4位有限域乘法規范的形式化描述是上述2個基本性質的合取,經過4次迭代運算得到最終結果,即:
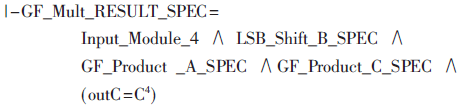
其中LSB_Shift_B_SPEC定義乘數InB從最低位開始的串行輸出值bi,Input_Module_4為輔助函數,定義數據的類型轉換。有限域乘法運算的最后結果即為outC=C(4)。
2.2 有限域乘法器實現的形式化建模
本文所研究的基于最低位優先算法有限域乘法器的電路實現如圖1所示[10],該系統通過比特串行的方式經過4個時鐘周期可完成4位有限域乘法運算。
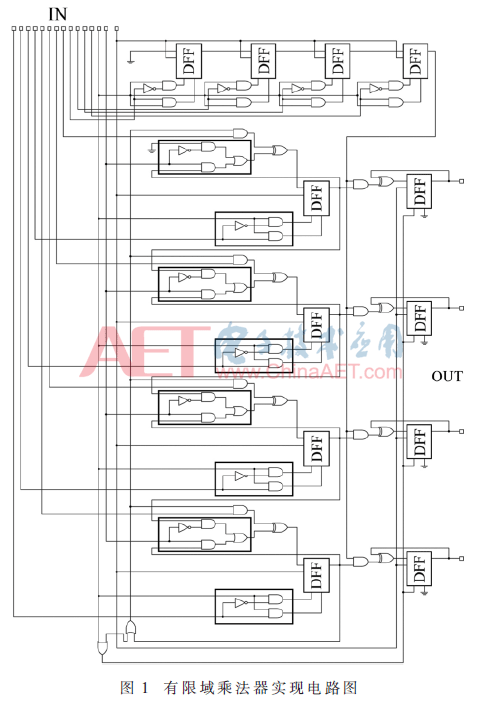
2.2.1 有限域乘法器電路結構分解
通常,對于加法器和譯碼器等規模較小、結構較為簡單的電路,可以直接通過邏輯“與”運算連接所有門電路完成電路實現的形式化建模。但是對于一個實現功能更為強大、規模更為龐大的電路實現,由于內部器件之間連線更為復雜,直接通過門電路合取進行建模容易由于人為的連接錯誤而導致模型錯誤,給驗證增加工作量;同時直接通過門電路合取構建的電路實現模型無法體現模塊間關系和電路結構特點,難以推導和證明實現電路蘊含目標性質。因此,為了驗證前述目標,本文采用自頂向下地對電路實現進行層次化分析和模塊化分解,依據實現的功能特性將整體電路劃分為若干模塊,然后將劃分得到的模塊進一步分解為若干的子模塊,直到不可再分解的基本單元結構。依據該方法分解的電路結構框圖如圖2所示。

總體上,有限域乘法器實現電路被分解為移位模塊和計算模塊兩大功能模塊。其中,移位模塊由若干個結構相同的移位基本單元所組成,用以實現式(4)中從最低位開始串行輸出乘數bi,移位基本單元又由D觸發器和初始化模塊所組成。計算模塊可進一步分解為計算A(x)模塊和計算C(x)模塊,分別對應實現式(3)和式(4)的運算功能。同理,這兩個子模塊也可由若干結構相同的更小子模塊所組成。
研究發現,有效的電路模塊分解有利于后續構建結構層次清晰的實現電路的形式化模型,這可使得驗證思路更加簡單明了,同時也縮小了驗證的規模,降低驗證難度。
2.2.2 有限域乘法器的電路時序分析
由于上述的有限域乘法器為同步時序邏輯電路,其任意時刻的輸出信號不僅與當前時刻的輸入信號有關,還與電路在輸入信號前的狀態相關,所以相比于傳統的組合邏輯電路驗證,其驗證難度更大。
圖1中電路實現的存儲元件為D觸發器,當直接依據觸發器特性進行建模時,建模和驗證的重心將偏向于時鐘信號波形的變化和輸入輸出狀態之間的關系,不利于對有限域乘法器功能的驗證。另外,在對電路特性和功能特性進行分析后發現,該電路是由統一的時鐘信號控制,只有時鐘信號出現觸發沿時,電路中各個變量的狀態才會發生變化,而在兩個相鄰時鐘信號的觸發沿之間,電路狀態是不會發生改變的,因而定義相鄰觸發沿的時間間隔為同步時序邏輯電路的一個運行周期,以周期作為時間抽象的最小粒度,可以有效地構建電路實現基于功能的形式化模型[11]。因此,本文采用基于周期的方法完成對同步時序邏輯電路的形式化建模。
D觸發器基于周期所實現的功能為:在任意周期內,當置位信號set為T時,觸發器進行置位操作,輸出信號out為高電平T;當復位信號reset為T時,觸發器進行復位操作,輸出信號out為低電平F;否則輸出信號out等于上一周期的輸入信號值inp,則基于上述方法D觸發器的形式化描述為:
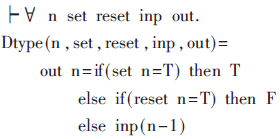
2.2.3 有限域乘法器實現的形式化建模
電路的形式化建模過程一般為電路結構模塊分解的逆過程:在基本單元結構完成描述的基礎上,開始自底向上地進行建模,在完成所有對應子模塊驗證后,再通過子模塊的驗證結果完成上一層次模塊的建模和驗證,并逐步地、層次化地完成有限域乘法器的形式化建模。為了更好地說明有限域乘法器實現的形式化建模過程,本節將以有限域乘法器中計算A(x)模塊的建模和驗證為例進行說明。
計算模塊是有限域乘法器中實現乘法運算的核心模塊,依據電路功能結構劃分,計算模塊可以分解為計算A(x)模塊和計算C(x)模塊,分別對應實現最低位優先算法中式(3)和式(4)的運算操作。
計算A(x)模塊由4個結構相同的計算A(x)模塊基本單元所組成,其基本單元實現按位對A(x)進行初始化置數、移位和取模運算操作。該基本單元模塊進一步由與門、異或門、初始化模塊、D觸發器和多路選擇模塊組成,其中初始化模塊和多路選擇模塊通過基本門電路組合實現。
初始化模塊的實現描述如下:

初始化模塊實現通過初始化信號init控制,依據輸入值in生成相應的置位信號set和復位信號reset,其規范表述為:

多路選擇模塊由基本門電路的組合實現,依據選擇信號sw選擇相應的輸入作為輸出的功能,實現的描述如下:

在完成相應子模塊建模和驗證的基礎上,通過子模塊的組合完成計算A(x)模塊基本單元實現的形式化建模,表述如下:

計算A(x)模塊基本單元所實現的功能為:在初始周期,對模塊進行初始化操作,輸出對應比特位的初始數值;其他任意周期,由模式信號mode控制選擇輸出有限域加法或者移位取模對應比特位的運算結果。
通過初始化模塊和多路選擇模塊的驗證結果,完成對計算A(x)模塊基本單元的正確性進行驗證:

又因為計算A(x)模塊由4個基本單元組合,故通過基本單元實現模型邏輯表達式的合取完成計算A(x)模塊的形式化建模,結果為:


同理,使用相同的方法也可完成對移位模塊和計算C(x)模塊的形式化建模和驗證,并驗證計算C(x)模塊實現電路蘊含有限域乘法規范中的性質2。最后得到的有限域乘法器實現的形式化描述如下:
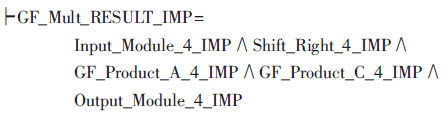
其中,Shift_Right_4_IMP表示移位模塊實現的形式化模型,GF_Product_A_4_IMP表示計算A(x)模塊實現的形式化描述,而GF_Product_C_4_IMP為計算C(x)模塊實現的形式化描述,Input_Module_4_IMP和Output_Module_4_IMP為輔助函數,定義數據的類型轉換。
3 有限域乘法器的形式化驗證
通過對有限域乘法器算法和電路實現的分析,完成對有限域乘法器性質規范和電路實現的形式化建模。為了進一步證明有限域乘法器設計的正確性,仍需在HOL4系統中完成有限域乘法器電路實現蘊含有限域乘法器算法規范的驗證,即:

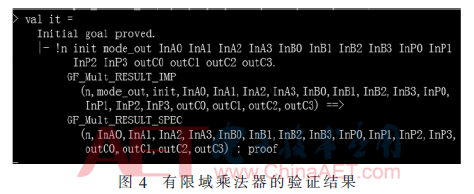
其在HOL4系統中的形式化描述如圖3所示。圖4為有限域乘法器在HOL4系統中的驗證結果,初始目標得證,說明有限域乘法電路實現可以正確地實現有限域乘法運算并輸出正確的運算結果。

4 結論
本文使用定理證明方法對有限域乘法器進行形式化驗證,并在形式化建模過程中提出了模塊分解和分層的思想,依據功能結構特點對電路實現進行自頂向下的分解,并自低向高地完成結構建模和逐層驗證。另外,依據電路的時序特點,提出了一種基于周期的形式化建模方法,有效映射了算法循環周期與電路時序周期的對應關系,該建模方法也可以應用到其他時序邏輯電路的建模和驗證中。
參考文獻
[1] LID`L R,NIEDERREITER H.Introduction to finite fields and their applications[M].New York:Cambridge University Press,2012.
[2] BIHAM E,CARMELI Y,SHAMIR A.Bug attacks[J].Journal of Cryptology,2016,29(4):775-805.
[3] MORIOKA S,KATAYAMA Y,YAMANE T.Towards efficient verification of arithmetic algorithms over Galois fields GF(2m)[C].Proceedings of the 13th International Conference of Computer Aided Verification.Paris,France:Spring,2001:465-477.
[4] MUKHOPADHYAY D,SENGAR G,CHOWDHURY D R.Hierarchical verification of Galois field circuits[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2007,26(10):1893-1898.
[5] LV J,KALLA P,ENESCU F.Efficient Grobner basis reductions for formal verification of Galois field multipliers[C].Proceedings of the Conference on Design,Automation and Test in Europe.Dresden,Germany:2012:899-904.
[6] LV J,KALLA P,ENESCU F.Efficient Grobner basis reductions for formal verification of Galois field arithmetic circuits[J].IEEE Transactions on Computer Aided Design of Integrated Circuits and Systems,2013,32(9):1409-1420.
[7] OKAMOTO K,HOMMA N,AOKI T.A graph-based approach to designing parallel multipliers over Galois fields based on normal basis representations[C].Proceedings of the 43rd International Symposium on Multiple-Valued Logic,Toyama,Japan:2013:158-163.
[8] PAAR C,PELZL J.Understanding cryptography:a textbook for students and practitioners[M].Berlin:Springer Publishing Company,2010.
[9] SARGUNAM B,ARUL MOZHI S,DHANASEKARAN R.High speed bit-parallel systolic multiplier over GF(2m) for cryptographic application[C].2012 IEEE International Conference on Advanced Communication Control and Computing Technologies.Ramanathapuram,India:IEEE Press,2012:244-247.
[10] ANDRONIC C,CHIPER D F.A unified VLSI architecture for addition and multiplication in GF(2m)[C].Proceedings of 2015 International Symposium on Signals, Circuits and Systems.Iasi,Romania:IEEE Press,2015:1-4.
[11] 周寧.代數化符號模擬驗證的應用研究[D].北京:北京交通大學,2015.

