文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.182981
中文引用格式: 張曉明,曹國清,陳增強,等. 基于AdaBoost-PSO-ELM算法的滑坡位移預測研究[J].電子技術應用,2019,45(2):84-87,92.
英文引用格式: Zhang Xiaoming,Cao Guoqing,Chen Zengqiang,et al. Landslide displacement prediction based on AdaBoost-PSO-ELM algorithm[J]. Application of Electronic Technique,2019,45(2):84-87,92.
0 引言
礦山排土場滑坡是一種非常普遍發生的地質災害,由于滑坡的頻繁發生,每年都會造成大量的人員傷亡和巨額的財產損失。很多排土場都存在著滑坡風險,排土場的堆放位置以及堆放方式和管理方式的不合適可能會造成滑坡事故的發生。隨著傳感器技術的發展,各種類型的傳感器相繼被應用到了礦山排土場的安全監測當中,傳感器能長時間保持不間斷地采集排土場的相關指標,這些相關指標對排土場的安全指標具有重大意義,在一定程度上體現著排土場的穩定狀態。傳感器傳輸的實時數據代表排土場的某一時刻相關特征指標的值,但是當技術人員接收到異常數據時,排土場滑坡或許已經發生了,若能夠提前預測出傳感器下一時刻的信息,可以有效降低排土場滑坡造成的財產損失和人員傷亡,到目前為止,礦山排土場滑坡災害預警仍然是一個處于探索階段的世界性難題[1]。
目前關于滑坡預測方法主要是分析滑坡位移隨時間變化的曲線及各類直接或間接影響滑坡產生的環境影響因子的監測信息[2],來反演滑坡內在的非線性動力學變化過程,進而建立起滑坡位移同各個環境影響因子之間的非線性映射關系,最終達到預測滑坡位移的變化趨勢的效果。傳統的滑坡預測模型主要以時間序列分析方法和各類統計方法預測為主[3],這些方法在智能性、精確性和及時性方面都存在著較大的缺陷。為了有效提高對滑坡的預測能力,本文提出了一種AdaBoost的粒子群優化極限學習機的集成學習方法實現滑坡位移預測(AdaBoost-PSO-ELM),與以往方法相比,其具有以下優點:(1)利用粒子群優化算法(Particle Swarm Optimization,PSO)來優化極限學習機(Extreme Learning Machine,ELM)的輸出權重和隱層偏置,解決了人工參數整定困難的問題[4],提高了預測效率;(2)采用多神經網絡集成學習算法,提高網絡預測泛化能力;(3)引入AdaBoost算法極大降低了ELM陷入局部最優的風險,進一步提高了預測精度。
1 算法分析與設計
1.1 極限學習機模型
極限學習機(Extreme Learning Machine,ELM)是HUANG G B等在2006年提出的一種單隱含層前饋神經網絡(Single Hidden Layer Feedforward Neural Networks,SLFNN)的算法,該算法隨機產生輸入層與隱含層的連接權值及隱含層神經元的偏置[5],構建無需任何迭代的單隱層神經網絡,與傳統神經網絡相比,通過一步計算即可解析出網絡的輸出權值,大大提高了網絡的泛化能力和學習速度,具有較強的非線性擬合能力。ELM的網絡結構如圖1所示。



1.2 粒子群優化算法
粒子群優化算法(Particle Swarm Optimization,PSO)的基本思想源于鳥群的覓食行為,每個粒子在初始階段都會被初始化為一定的速度、位置和一個由適應度函數決定的適應值,同時每個粒子都被賦予記憶功能。在每一次迭代尋優的過程中,粒子通過比較適應度值和兩個邊界值來更新自己的速度和位置,通過不斷的更新速度和位置,粒子本身最終能找到個體最優解和整個種群全局最優解[6]。
利用動態慣性權重ω的方法提高粒子群的尋優能力進而加快極限學習機(ELM)的預測效率和提高預測精度,較高的慣性權重ω會使粒子群算法有更好的全局的尋優能力,而較低的慣性權重ω則對于局部尋優效果更好[7],粒子速度和位置更新表述如下:

本文中以實際值與預測值的均方誤差(MSE)作為粒子尋優的適應度函數[8]:

利用PSO尋找ELM中最優的隱含層節點數、輸入權值和隱含層偏置,使獲得的模型更能準確預測滑坡的地表位移。
1.3 AdaBoost的粒子群優化極限學習機算法(AdaBoost-PSO-ELM)設計
AdaBoost算法是Boosting思想的機器學習算法,其核心思想先從初始訓練集訓練出一個基學習器,根據基學習器的表現對訓練樣本進行調整,使得先前基學習器做錯的訓練樣本在后續受到更多的關注,然后基于調整后的樣本分布來訓練下一個基學習器,重復進行,直至基學習器數目達到指定的值[9]。
本文提出的AdaBoost-PSO-ELM算法基本思想是:初始化一個ELM基學習器,反復訓練得到多個ELM的弱預測器,使用AdaBoost算法將得到的多個ELM弱預測器組成一個強預測器,進一步提高ELM網絡的預測準確率,降低ELM網絡陷入局部最優的風險[10],提高ELM的泛化能力。AdaBoost-PSO-ELM算法流程如圖2所示。其詳細步驟如下:

(1)給定輸入樣本。對ELM網絡、PSO相關參數進行初始化,從輸入樣本數據中選取訓練集中的m組數據,初始化測試數據分布權值D1=(1/g,…,1/g)1×m,根據輸入輸出樣本的特性指標維度確定ELM網絡結構。
(2)輸入樣本數據預處理。其中包括異常值處理、空缺值填補、無量綱化等,對異常值作為缺失值處理,通過拉格朗日插值法對所有空缺值進行插值填補;排土場數據集中每個特性指標間的單位存在量綱差異,為消除不同量綱間對預測精度的影響,對排土場數據進行無量綱化處理[11];
(3)通過PSO優化ELM的輸入參數,同時得到多個ELM弱預測器,在訓練第n個ELM弱預測器時,使用ELM對訓練集數據進行訓練,得到預測序列的預測誤差和errorn,誤差和errorn的公式如式(10)所示:


2 試驗研究與結果分析
為驗證本文提出的AdaBoost的粒子群優化極限學習機算法的有效性和準確性,采用中國貴州某礦山排土場在2016年12月~2017年11月間從傳感器中采集到的該礦山排土場的各特性指標數據,各指標數據每隔半小時到一小時更新一次,總共含有14 423條數據,其中被選取的特性指標有地表位移(Mp)、土壓力(Dm)、土壤含水率(Smc)、降雨量(Rg)、孔隙水壓力(St)、濕度(Hum)、溫度(Tpr)、內部位移(Ep)共8個指標。
8個指標中,地表位移是最直觀、最能反映排土場邊坡變化趨勢的觀測性指標;邊坡內部位移最能反映滑坡體多層變形和滑帶的位置,是滑坡監測的一個非常重要的監測對象;同時降雨量、土壤含水率、土壓力、孔隙水壓力、濕度和溫度也會直接或間接地影響到前面指標的變化。本文將地表位移作為判斷排土場滑坡的直接因素,其余特性指標作為間接判斷排土場滑坡的綜合因素。本文主要進行了3個模型的驗證分析,將數據集的前70%作為訓練數據,后30%作為驗證數據,以均方根誤差(RMSE)作為性能評價指標。

本文做了3組對比試驗,分別為ELM、PSO-ELM、AdaBoost-PSO-ELM模型對地表位移的預測,其他7個特性指標作為目標的輸入。首先,采用ELM進行地表位移的預測,圖3所示的是ELM對地表位移的預測效果曲線圖,該模型隨機初始化一組輸入權值和隱含層偏置,采用sigmoid函數作為激活函數,神經元的個數為100,從圖中可以看出,預測效果不是很好,RMSE的值為2.89。

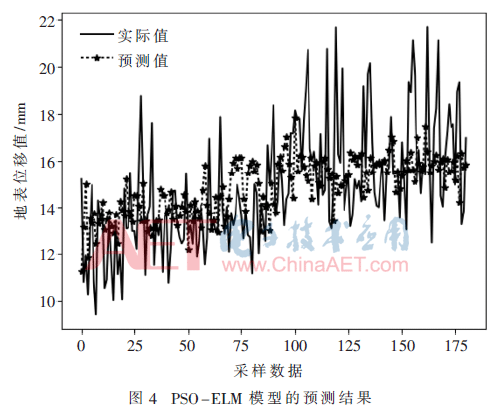
為避免ELM輸入參數隨機化,利用PSO得到ELM的輸入權值和隱含層偏置,種群為100的粒子群,其預測效果如圖4所示,預測效果比ELM網絡有了一定的提高,同時也基本擬合了真實曲線的趨勢,其RMSE的值為2.62,但是在精度方面還有上升的空間。圖5表示的是PSO在尋優過程中的迭代次數和均方誤差的關系,從圖中可以看出在迭代的初期,粒子群的收斂速度很快,變化率很大,隨著迭代次數的增加,粒子群的收斂速度趨于平緩,PSO在尋優過程中迭代到100次左右已開始收斂。

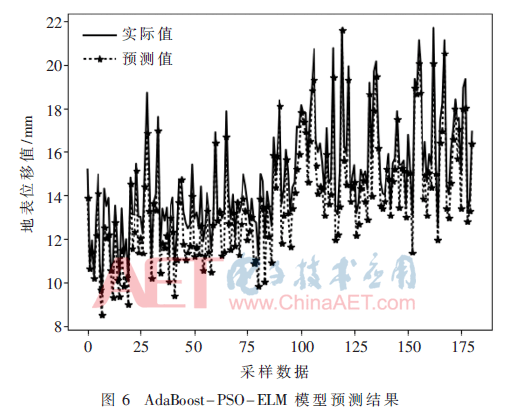
PSO尋優過程無法完全避免種群陷入局部最優風險,本文提出在PSO優化ELM的基礎上,采用AdaBoost算法進一步提升ELM預測的準確性,構造10個由ELM組成的弱預測器,利用AdaBoost算法將10個ELM弱預測器構成一個強預測器。實驗結果表明,該方法可以大幅度提升ELM預測精度,如圖6所示,從圖中可以發現經AdaBoost的粒子群優化的預測值與真實值的曲線趨勢基本處于同步,真實值與預測值曲線的間隔比起前兩種模型處理的效果有明顯的提高,預測結果能很好地擬合真實值,其RMSE的值為1.17。3組對比實驗的RMSE如表1所示。

3 結論
礦山排土場滑坡的過程是一個動態、大延遲、高度非線性的特性問題,影響礦山排土場滑坡的因素眾多,同時PSO無法避免陷入局部最優風險。對此,本文提出AdaBoost-PSO-ELM算法構成的強預測器方法,利用PSO算法確定了ELM的輸入權值,提高了ELM的學習效率,解決了人工參數整定難的問題。本文的具體思路是將ELM作為基學習器,經過反復訓練ELM的預測輸出,得到由多個ELM的弱預測器組成的強預測器。實驗結果表明,該方法具有較高的預測精度,有效地提高了礦山排土場滑坡位移預測精度。
參考文獻
[1] 秦宏楠.紫金山金銅礦排土場滑坡誘發機理及監測預警技術研究[D].北京:北京科技大學,2016.
[2] 張艷博,張國鋒,田寶柱,等.露天煤礦邊坡穩態影響因子敏感性分析及滑坡控制對策[J].煤炭工程,2011,1(5):105-107.
[3] 徐峰,汪洋,杜娟,等.基于時間序列分析的滑坡位移預測模型研究[J].巖石力學與工程學報,2011,30(4):746-751.
[4] 楊向萍,吳玉丹.基于PSO-BP神經網絡的人體穴位定位系統設計[J].電子技術應用,2018,44(9):75-78.
[5] HUANG G B,WANG D H,LAN Y.Extreme learning machines:a survey[J].International Journal of Machine Learning & Cybernetics,2011,2(2):107-122.
[6] 楊錫運,關文淵,劉玉奇,等.基于粒子群優化的核極限學習機模型的風電功率區間預測方法[J].中國電機工程學報,2015,35(S1):146-153.
[7] 李艷,楊華芬.一種改進的動態慣性權重粒子群優化算法[J].長春工程學院學報(自然科學版),2014(4):116-119.
[8] ABREU L D,ROMERO J L.MSE estimates for multitaper spectral estimation and off-grid compressive sensing[J].IEEE Transactions on Information Theory,2017,PP(99):1.
[9] GUO H,LI Y,LI Y,et al.BPSO-Adaboost-KNN ensemble learning algorithm for multi-class imbalanced data classification[J].Engineering Applications of Artificial Intelligence,2016,49(C):176-193.
[10] 趙英剛,龔壘.基于行為識別和SVM的短信過濾方法研究[J].微計算機信息,2012(1):176-177.
[11] 曹國清,張曉明,陳亞峰.基于PCA-LSTM的多變量礦山排土場滑坡預警研究[J].計算機系統應用,2018,27(11):252-258.
作者信息:
張曉明1,曹國清1,2,陳增強1,何佳康1,2
(1.北京石油化工學院 信息工程學院,北京102617;2.北京化工大學 信息科學與技術學院,北京100029)

