0  引言

    電壓、頻率、有功功率、無功功率是電力系統最重要的電氣量，它們之間存在著復雜的關系。一般來說，頻率與有功功率關系大。當系統有功出現缺額(發出的有功少于消耗的有功)時，頻率就會下降，頻率下降會使負荷消耗的有功減少；當系統有功出現過剩(發出的有功多于消耗的有功)時，頻率就會升高，頻率升高會使負荷消耗的有功增加。電壓與無功功率關系大^[1]。當系統無功出現缺額(發出的無功少于消耗的無功)時，系統電壓就會下降；當系統無功出現過剩(發出的無功多于消耗的無功)時，系統電壓就會升高。它們之間也會互相牽連和影響。例如，線路輸送有功增加也會引起電壓損耗增加，使線路末端電壓下降；頻率降低，會引起異步電動機和變壓器的勵磁電流增加，所消耗的無功增加，從而使電壓下降；系統電壓升高或降低會使負荷消耗有功增加或減少，從而影響頻率變化。分析電力系統出現的一些現象，要分清主次，才能得出正確結論。

1  系統正常運行頻率質量和經濟問題

    頻率不僅是電力系統運行與表征電能質量的重要指標，而且是電力系統運行的重要參數^[2]。我國電力系統頻率額定值為50 Hz。頻率過大或過小都會影響產品的質量乃至整個電力系統的穩定性，從而造成嚴重的經濟損失。電力系統中的發電、變電、輸電、配電和用電設備是按額定頻率進行設計和制造的，這些設備在額定頻率下運行，其效能最佳。當頻率偏離額定值，將影響電力用戶產品的數量和質量，嚴重是會造成廢品，導致用電設備無法正常工作，此外還會影響電力系統本身的正常運行和安全運行。當頻率降低時，會造成汽輪機葉片振動增大，降低其壽命，有時會造成共振，使葉片斷裂；同時還會造成由異步電動機驅動的電廠廠用電機械出力下降，導致發電機出力下降，使系統頻率進一步下降，從而出現頻率崩潰現象^[3]。有核電站的電力系統，頻率偏移過大會使反應堆冷卻介質泵自動斷開，從而導致反應堆停止運行^[4]。當頻率過高時，也會影響大容量汽輪機葉片和大軸的壽命，因此頻率過高也應引起注意^[5]。另一方面，系統頻率降低時，異步電動機和變壓器的勵磁電流增加，所消耗的無功功率增大，結果引起電壓下降，當頻率降至45~46 Hz時，發電機和勵磁機轉速均顯著下降，導致各發電機的電動勢下降，全系統的電壓水平大為降低，如果系統原來的電壓水平偏低，還可能引起電壓不斷下降，出現電壓崩潰現象。發生頻率或電壓崩潰，會使整個系統瓦解，造成大面積停電^[6]。

2  負荷的頻率靜態特性及負荷與頻率的關系

    系統處于運行穩定時，系統中負荷的有功功率隨頻率的變化特性稱為有功功率-頻率靜態特性，簡稱負荷的頻率靜態特性。根據所需的有功功率與頻率的關系可將負荷分成以下幾類：

    （1）不受頻率影響的負荷，如白熾燈、電熱器、照明、電熱和整流負荷等。

    （2）與頻率成正比的負荷，通常負荷的阻力矩等于常數的屬于此類，如帶金屬切削機床和磨粉機的電動機、球磨機、往復式水泵壓縮機和卷揚機等。

    （3）與頻率的二次方成正比例的負荷，如網損、變壓器中的渦流損耗。

    （4）與頻率三次方成正比的負荷：如通風機、靜水頭阻力不大的循環水泵等。

    （5）與頻率的高次方成正比例的負荷，如靜水頭阻力很大的給水泵等。

    系統實際負荷是上述各類負荷的組合，稱為綜合負荷，其有功功率與頻率的關系可以表示為：

    上式表示負荷有功功率與頻率呈非線性關系。當頻率下降時，負荷有功功率將減少；當頻率升高時，負荷有功功率將增加^[7]。這就是說，當系統有功功率失去平衡而引起頻率變化時，系統負荷也參與對頻率的調節，其特性有助于系統有功功率在新的頻率下重新獲得平衡，這種現象稱為負荷的頻率靜態調節效應。負荷的頻率靜態調節效應一般用負荷的頻率靜態調節效應系數表示，它等于負荷有功功率標幺值的變化量與頻率標幺值的變化量的比值^[8]，即

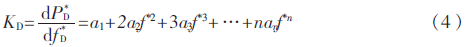
    不同電力系統負荷頻率靜態調節效應系數不同，同一系統不同時間段負荷頻率靜態調節效應系數也不同。當系統出現功率缺額(或過剩)時，可利用K_D系數估算出系統頻率下降(或上升)值，這是調度中心必須掌握的運行參數^[9]。

    發電機也有頻率靜態調節效應，用系數K_G表示，它由調速器調差系數決定，即 K_G=1/δ_G。發電機頻率調節效應與負荷相反，當頻率下降(或升高)時，發電機輸出有功功率增大(或減小)，這有利于系統有功功率平衡和頻率的穩定。因此：

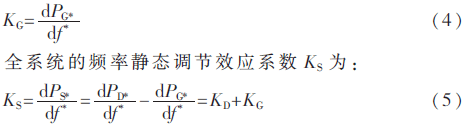
    當發電機滿載時，系統頻率下降，發電機頻率靜態調節效應幾乎不起作用。

3  電力系統頻率調整方式

    為了保持電力系統頻率在額定值附近運行，電力系統在正常運行方式下有三種調頻手段：

    （1）一次調頻。依靠發電機組的調速器調頻。當系統負荷發生變化，造成機組輸入功率與輸出功率不平衡后，會引起機組轉速發生變化，即頻率發生變化，隨后各機組的調速器會反應頻率的變化，自動地調節進汽(水)閥門的開度，改造機組出力，是系統有功功率重新達到平衡^[10]。這種調頻方式是所有的發電機組(除了系統頻率下降時的滿載機組)都參與調頻，但不可能是頻率恢復到原有值^[11]。

    （2）二次調頻。依靠發電機組調速器的同步器(調頻器)進行調頻。機組調速器的同步機由伺服電動機等元件組成，控制伺服電機的正反轉，就可調整轉速的整定值，相當于平移發電機調速器調差特性曲線(功率-頻率特性曲線)。裝有自動發電控制系統(AGG)的電廠，可以通過AGG達到自動二次調頻的目的。這種調頻方式只有部分機組參與調頻，且調頻可以恢復到原有值^[12]。

    （3）三次調頻。根據電力系統經濟調度原則分配各發電機的有功功率，稱為三次調頻^[13]。這種調頻不僅能使頻率在額定值下運行，還能使電力系統處于最經濟狀態下運行。這種調頻方式由調度中心能量管理系統(EMS)來完成^[14]。因種種原因，目前只有少數電力系統實現三次調頻。

    與頻率靜態調節效應一樣，也有電壓靜態調節效應，因為負荷消耗的無功功率與電壓也有零次方、一次方、二次方和多次方關系的，這表示負荷消耗的無功功率與電壓也成非線性關系^[15]。當電壓下降時，負荷無功功率將減少；當電壓升高時，負荷無功功率將增加。這就是說，當系統無功功率失去平衡而引起電壓變化時，系統負荷也參與對電壓的調節，其特性有助于系統無功功率在新的電壓下重新獲得平衡，這種現象稱為負荷的電壓靜態調節效應。同理，也有發電機的電壓靜態調節效應。與頻率靜態調節效應不一樣，電壓靜態調節效應很難找到一個全網靜態調節效應系數，因此對此分析研究很少。

4  基于PSASP實際電網模型的算例分析

    本電網是基于某實際電網中的局部電網搭建的電網模型，PSASP軟件的仿真就是基于此局域電網進行的^[16-17]。該電網的系統基準容量是1 000 MVA，下面介紹一些用PSASP軟件的電網模型搭建與仿真成果。

    （1）切除發電機

    切除發電機后，總發電機的出力減小，當發電機出力小于負荷(包括網損)需求時，使發電機轉速下降，系統頻率降低，一方面由于發電機調速器作用，其出力略有增加，另一方面負荷有功功率與頻率有關，頻率下降時負荷消耗的有功功率略有減少，從而使供需達到新的平衡，也就是在較低的頻率下平衡。

    PSASP仿真中選擇切除發電機天光G5，仿真結果如圖1所示。

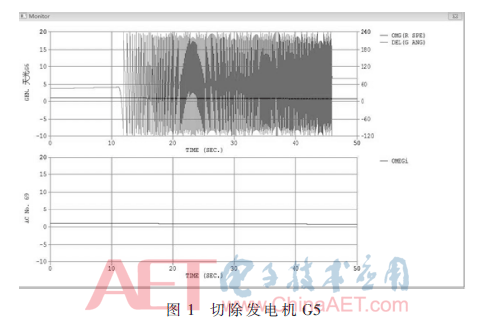
    仿真觀測的電氣設備的數據是發電機天光G6的功角、天光G6的頻率以及69號線路hm天光1101-hm天光1102的交流線的頻率。從圖可知，切除發電機后，發電機的功角出現了一段時間的震蕩，其頻率逐漸降低到趨于平衡，69號交流線的頻率逐漸降低到趨于平衡。從而切除發電機后相當于整體發電機出力不足，這時候根據前面發電機與負荷頻率特性分析可知電力系統頻率將降低。

    （2）切除線路

    切線路對電力系統頻率的影響要分情況討論不可一概而論，對于接近電廠的線路，承擔著將電廠發電輸送出去的艱巨使命，這些線路一般會有非常大的潮流，切除這些線路將對電力系統造成非常大的影響，可能會造成整個電力系統的崩潰，發電機被迫停機等事故。所以一般這些線路要特別的注意與保護，為了安全起見，這些線路一般采用多回線路輸送，減小故障對電力系統的影響。這些線路一般也不可切除，除非在發電機停機，線路檢修時才行，否則，線路一切斷，發電機發電很多都沒法輸送出去，發電機的頻率就會節節上升，嚴重時會造成飛輪事故，給生命安全帶來隱患，整個發電機也將報廢。

    如圖2就是切除這樣一條線路，104號輸電線東疆220-天光2201后對系統的仿真。

    從圖可知，發電機天光G6的功角在一段時間內出現震蕩，頻率節節上升，69號線路的頻率也出現震蕩。整個電力系統崩潰無法正常運行。

    還有一類線路離發電廠較遠，承擔著一定量的負荷潮流的輸送，這種線路接近于負荷特性，切除這種線路相當于切負荷會造成電力系統頻率上升。如圖3所示，切除兩條線路：線路66(hm天光1101-hm北郊1101)和線路70(hm天光1102-hm馬場110)的仿真。

    可見發電機功角一段時間內出現震蕩，發電機頻率增加最后達到穩定，頻率穩定在一個較高水平。69號線路的頻率也先增加最后穩定在一個較高的水平。

    （3）切除負荷

    電力系統的電能是不能儲存的，有功功率供需關系一定要保持平衡。當發電機出力大于負荷(包括網損)需求時，使發電機轉速上升，系統頻率升高，一方面由于發電機調速器作用，其出力略有減少，另一方面負荷有功功率與頻率有關，頻率升高時負荷消耗的有功功率略有增加，從而使供需達到新的平衡，也就是在較高的頻率下平衡。正常情況下切除負荷，就會使發電機的出力大于負荷，從而導致電力系統的頻率升高。

    如圖4切除負荷hm一電35(0.005+j0.002)后的仿真。

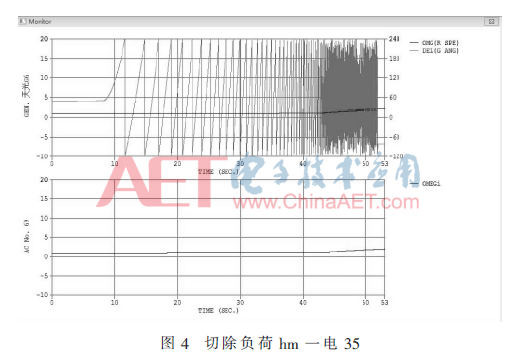
    可見電力系統頻率上升達到新的穩定值。

    但也有些情況切負荷，會使系統頻率降低，其實這也是不足為怪的，仿真結果也是正確的。電力系統頻率決定因素很多，決定過程亦是一個復雜的過程，它不僅要受到負荷有功功率的影響也受到負荷無功功率的影響。假設線路輸送的潮流是P+jQ，切除的負荷為P_L+jQ_L，切除后線路輸送潮流為(P-P_L)+j(Q-Q_L)，線路輸送的無功功率減少。由于電力系統決定因素很多是非線性的，若此時無功為主要決定因素，由于無功負荷被切除，切除后電力系統中的無功供應相對比未切除前的充足，會引起電力系統電壓升高，從而導致負荷消耗有功增加，當增加的負荷消耗有功的量大于線路切除的有功的量時，則會導致發電機出力小于負荷需求。從而由發電-負荷功率頻率特性曲線可知經過發電機一系列調節過程后，會使頻率降低，在較低的頻率中發電與負荷達到新的平衡。

    圖5切除負荷hm天光351(0.01+j0.0033)就是這種情況。從圖5可知，切負荷后電力系統電壓升高，頻率降低。

    （4）沖擊負荷

    沖擊負荷是具有周期性或非周期性，突然變化很大的負荷。如電弧煉鋼爐、軋鋼機等。一般出現最大負荷的時間很短，但其峰值可能是其平均負荷的數倍或數十倍。這類負荷對電力系統影響較大，當其變化幅值相對于系統容量較大時，很有可能引起系統頻率的連續振蕩，電壓擺動。通常對沖擊負荷需要做專門的研究，并提出相應的對策，以滿足電力系統安全穩定和電能質量的要求。圖7對負荷母線hm巴變101進行沖擊負荷仿真的情況。

    從以上兩圖可知在1 s到1.4 s之間對母線hm巴變101施加了一個尖頂狀得沖擊負荷，該過程中電力系統的頻率與電壓都出現了一些波動，隨著沖擊負荷的消失電力系統再次達到了穩定狀態。說明該系統的抗沖擊負荷的能力還是比較強的，由于天光G6離沖擊負荷母線較遠所以影響比較小，而201號交流線由于離沖擊負荷比較近所以影響比較大。

5  結論

    頻率變化的原因是電力系統中負荷的變化，也即頻率變化是系統負荷與電源之間的功率失去平衡所致，確切的說有功功率有著更為直接的影響作用。當系統有功出現缺額(發出的有功少于消耗的有功)時，頻率就會下降，頻率下降會使負荷消耗的有功減少；當系統有功出現過剩(發出的有功多于消耗的有功)時，頻率就會升高，頻率升高會使負荷消耗的有功增加。所以系統中會影響到負荷以及負荷中有功與無功比例的因素都會影響到電力系統的頻率特性。所以，電力系統的電壓水平、有功功率、無功功率、切機、切負荷、切線路、沖擊負荷、勵磁、發電機慣性時間常數、調速器調差系數、調速器死區、調速器汽門開度、動態負荷恒定阻抗的比例、感應電動機參數、發電機剩余參數,調速器剩余參數等等都是影響電力系統頻率特性的因素。

    對于電力系統低頻與高頻問題，若電力系統頻率偏高，可以采用切除一部分機組或者利用調速裝置調節發電機轉速；頻率過低，可以進行低頻減載方案設計切除部分負荷(負載)或者利用調速裝置調節發電機轉速。除此之外對頻率問題還可以用調頻器進行調節或者進行頻率控制的設置與規劃。

參考文獻

[1] 毛叔鈞，曾家瑞.電力系統頻率特性的實用分析法[J].電力系統自動化，1990,10 (5) :12 - 15．

[2] 孟祥萍，高嬿. 電力系統分析[M]. 北京: 高等教育出版社, 2004: 53-56．

[3] 馬大強. 電力系統機電暫態過程[M]. 北京: 水利電力出版社, 1988: 107-111．

[4] Olle E. Electric Energy Systems Theory-An Introduction[M]. Second Edition, New York: Mc Graw-Hill Book Company, 1982:156-161．

[5] Cohn N Control of Generation and Power Flow on Systems [M]. John Wiley and Sons, Inc. 1971: 35-39．

[6] Analysis and Modelling Needs of Power Systems Under Major Frequency Disturbance CIGRE 1999: 3-5．

[7] Kennedy T, Stephen M, Hoyt. Variable, Non-Linear Tie-Line Frequency Bias For Interconnected Systems Control. IEEE Transactions on Power System. 1988, 3(3): 123-125．

[8] 杭乃善，周航，李如琦．穩態控制潮流的設定空載頻率及空載電壓算法[J]．中國電機工程學報, 2003, 23(12)：74-78．

[9] TAYLOR C W. Conception of undervoltage load shedding for voltage stability [J]. IEEE Trans on Power Delivery ,1992,7(2):480- 488．

[10] Tuan T Q, Fandino J. Emergency load shedding to avoid risks of voltage instability using indicators[J]. IEEE Trans on Power Delivery, 1994, 9(1) :341-351．

[11] GRANVILLE S, MELLO J C, MELO A C G. Application of interior point methods to power flow unsolvability [J]. IEEE Trans on Power System, 1996, 11(2) :1096-1103．

[12] Ar nborg S, Andersson C, Hill D J. On undervoltage load shedding in power system [J]. Int J Elect Power Energy Syst, 1997, 19(2):141-149．

[13] Ba lanathan R, Cpaha lawath N. Under voltage load shedding to avoid voltage instability[J].IEE Proc Gener Transm Distrib,1998, 145(2) : 175- 181．

[14] Xu W, Mansour Y. Voltage stability analysis using general dynamic load models[J]. IEEE Trans on Power System, 1994, 9(1) : 479- 493．

[15] Ju P, Rehtanz E. A comparative study on the nonlinear dynamic load models[C]. Proc of PSCC 96，Dresden, Germany. 1996．

[16] 中國電力科學研究院計算所. PSASP潮流計算用戶手冊. 北京: 電力系統分析綜合程序室, 2003: 1-27. 

[17] 中國電力科學研究院計算所. PSASP暫態穩定計算用戶手冊. 北京: 電力系統分析綜合程序室, 2003: 25-36.

作者信息:

劉杰鋒，李  冰，張  帆，王  帥，段正陽，林宇龍，劉  芳

（國網冀北電力有限公司經濟技術研究院，北京 100038）