0 引言

    近年來，復雜網絡引起了科學家的廣泛關注^[1]。復雜網絡最重要的統計特征是小世界效應^[2]和無標度特性^[3]，其中，小世界網絡具有小的特征路徑長度和大的簇系數，而無標度特性指的是網絡的節點度(節點的度定義為與該節點相關聯的邊的條數)分布服從冪律^[4]。

    復雜網絡上的同步現象是一種重要的研究課題^[5-7]。研究表明，無標度網絡和小世界網絡的同步能力好于規則網絡^[8]。對這一現象的普遍解釋是小世界網絡和無標度網絡的平均最短距離小，使得信息之間的交流更高效。然而本文發現網絡的同步能力幾乎獨立于網絡的平均路徑長度，即平均路徑相同的網絡同步能力卻存在較大的差異。NISHIKAWA T、MOTTER A E等的研究表明，對無標度網絡而言，網絡度分布的不均勻性抑制了網絡同步能力的增強^[9]；HONG H、KIM B J等的研究則表明，對WS小世界網絡而言，使節點度分布變得不均勻(即增大度分布的方差)增強了小世界網絡的同步能力^[10]，與文獻的結論貌似沖突。本文對此給出了詳盡的解釋。

    BARAHONA M和PECORA L M^[11]研究了線性耦合網絡的同步穩定性問題，給出了主穩定函數判據。如果在網絡的每個節點上放置一個動力學系統(該動力學系統既可以是極限環，也可以是混沌的)，讓有邊相連的兩個節點的動力學系統之間存在相互耦合作用，就形成了一個動力學網絡。設網絡有N個節點,那么第i個節點所滿足的狀態方程是：

    WS小世界網絡的構造算法為：(1)給定一個節點數為N的規則網絡，每個節點都與它最鄰近的K=2k個節點相連，通常N≥K≥1；(2)依次訪問網絡中的每個節點，對每個節點的所有連線以概率p進行重連，連接該節點的一端不變，另一端隨機選擇節點連接，但兩個節點之間不允許重復連接，也不允許節點與自身相連。

    本文考慮了一種擇優選擇的小世界網絡模型(Small-World Networks with Preferential Attachment，PA小世界網絡)。其構造算法為：(1)步驟(1)與WS小世界網絡模型相同；(2)在WS小世界網絡斷開重連時，不是隨機選擇一個節點連接，而是按照正比與節點度的概率選擇節點連接。

1 網絡幾何特征量

1.1 簇系數

    簇系數是表征網絡節點集群程度的物理量。節點i的簇系數定義為所有相鄰節點之間連邊的數目與可能的最大連邊數目的比例。假設節點i的度為k_i，它的所有鄰居節點之間的邊數為E_i，則節點i的簇系數定義為C_i=2E_i/(k_i(k_i-1))。對網絡中所有節點的簇系數求平均值就是整個網絡的簇系數。

1.2 特征路徑長度

    在網絡中，兩點間的距離定義為連接兩點的最短路徑所包含的邊的數目，對所有節點對的距離求平均就得到了網絡的特征路徑長度。

1.3 節點度的方差

    節點度的方差是衡量節點度分布均勻性的一種度量。度分布越均勻，方差越小；反之，方差越大。其定義為：

1.4 節點的介數

    節點k的介數定義為：

式中，g_ij是節點i和節點j之間最短路徑的條數，g_ikj表示節點i和節點j之間最短路徑中經過節點k的條數。對網絡中的所有節點對(i，j)求和即可以得到節點k的介數。由此可以看出，一個節點的介數反映了該節點在其他節點通信中的重要程度。

2 仿真結果

    仿真中，選擇網絡節點數N=500(仿真表明，節點數的多少并不影響結果的普遍性)，K=2k=12，即網絡的平均度<k>=12。仿真圖的數據為節點數N=500時程序運行50次的平均結果。

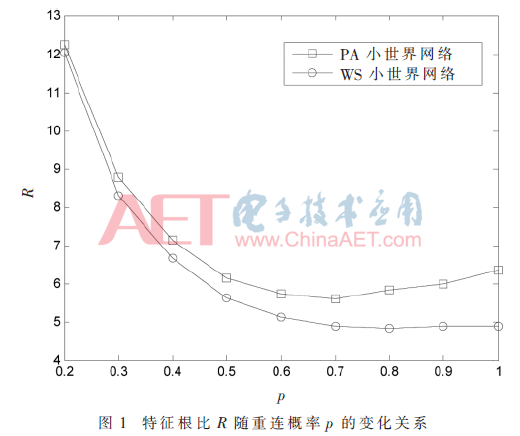
    首先研究了特征根比例R隨重連概率p的變化情況。如圖1所示，對于PA小世界網絡，隨著的p增大，R值先是單調減小然后單調增大，表明該網絡的同步能力隨著p先增強后減弱；對于WS小世界網絡，R單調遞減，這表明WS小世界網絡的同步能力隨著p的增大而增強。那么發生這種差異的原因是什么呢？為此，本文還研究了網絡的其他幾何特征量，如網絡的特征路徑長度l和簇系數C(如圖2所示)、節點度的方差σ²(如圖3所示)、節點的最大介數B_max(如圖4所示)以及節點的最大度數k_max(如圖5所示)等隨著p的變化情況。

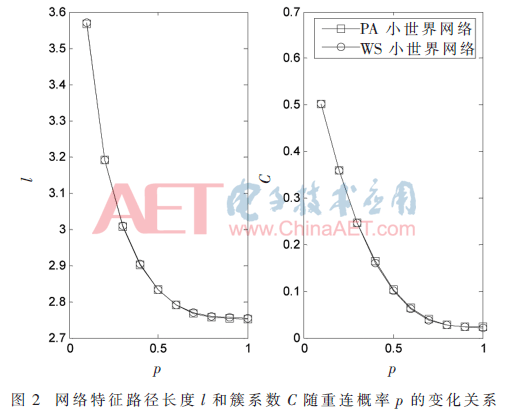
    由圖2可以看出，對于PA小世界網絡和WS小世界網絡，特征路徑長度l和簇系數C都隨著p的增加而單調減小，且幾乎保持一致，這說明圖1中R值的差異不是由特征路徑長度l和簇系數C的不同引起的；同時，也表明對于特征路徑長度和簇系數都幾乎相同的網絡，其同步性能仍然可以展現出相當的差異，也說明了兩者中的任何一個都不是造成這種差異的原因。

    圖3是對PA小世界網絡和WS小世界網絡的節點度的方差仿真的結果。顯而易見，PA小世界網絡和WS小世界網絡的節點度的方差都隨著p的增大而增大，但在PA小世界網絡中，由于重連時另一端為擇優選擇，導致節點度的方差增大的速度明顯快于WS小世界網絡。HONG H^[10]等人認為小世界網絡中節點度的方差的增大會導致其同步能力的增強。本文的仿真也表明，在WS小世界網絡中，隨著p的增大，R逐漸減小，節點度方差σ²逐漸增大，那么是否節點度的方差的增大是導致網絡同步能力增強的原因呢？答案是否定的。可以看到，在PA小世界網絡中，隨著重連概率p的增大，方差也逐漸增大，且增加的速率明顯大于WS小世界網絡，但由于節點度的方差增加的太快，使得這種度分布的不均勻性對網絡的同步能力起了抑制作用(如在圖1中當p≥0.7時R值的上揚，表明了PA小世界網絡同步能力的下降)。從圖1可以看出，在整個p值的范圍內，PA小世界網絡的同步能力明顯不及WS小世界網絡(因為R_PA>R_WS)。

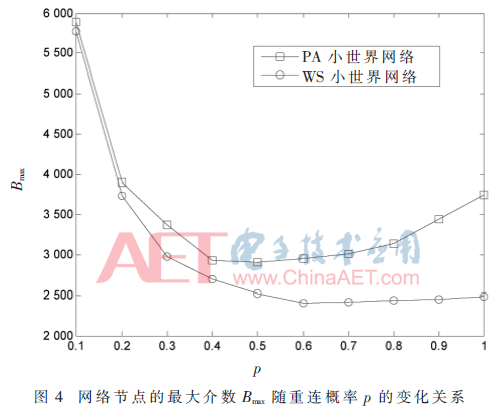
    另由圖3可知，在整個p值的范圍內，PA小世界網絡的節點度的方差始終大于WS小世界網絡。因為兩種網絡的網絡特征路徑長度l和簇系數C幾乎相等(由圖2可知)，由此可以推斷，節點度的不均勻性實際上對網絡的同步能力起抑制作用。由此，在WS小世界網絡中，增強網絡同步能力的主要因素不是節點度方差逐漸增大(節點度方差只是由于小世界網絡中邊的重連引起的一種很自然且必然的結果)，網絡的特征路徑長度下降才是最主要的原因(當p值較小時，盡管度分布的不均勻性抑制了網絡的同步能力，但由于網絡的特征路徑長度大幅下降，網絡的同步能力還是增強了；但是，當網絡的特征路徑長度下降幾乎為常數時，如果節點度分布的方差大于一定的臨界值，其抑制作用就比較明顯了，如圖1和圖3所示)。所以，短的特征路徑長度和均勻的節點度分布綜合作用才能導致網絡同步能力的增強。此外，NISHIKAWA T^[9]和HONG H^[10]均認為網絡節點的最大介數B_max是表征網絡同步能力的一種相對合理的因素。降低網絡節點的最大介數B_max將導致網絡同步能力的增強。圖4的仿真結果也說明了這個問題。可以看到，在PA小世界網絡中，B_max隨p先是單調下降然后單調上升，與R隨p的變化趨勢相同。所以，網絡中節點的最大介數B_max的確可以作為表征網絡同步能力的一種度量。

    由圖4可知，在整個p值范圍內，PA小世界網絡中節點的最大介數始終大于WS小世界網絡中節點的最大介數；而圖1中，在整個p值范圍內，PA小世界網絡的同步能力始終不及WS小世界網絡，這從另外一個側面反映了最大介數表征網絡同步能力的合理性。在無標度網絡中，網絡中最大節點度k_max和最大介數B_max是正相關的，即k_max越大，通常B_max也越大；在WS小世界網絡中，變化呈相反的趨勢，隨著k_max的增大，B_max單調下降，如圖4和圖5所示，在PA小世界網絡中，k_max和B_max呈現一種相對微妙復雜的關系。

3 結論

    本文研究了一種擇優選擇的小世界網絡模型，基于這種模型，詳盡地研究了網絡的同步能力與網絡中的各種幾何特征量(如網絡平均路徑、簇系數、度分布以及介數等)之間的關系。研究結果表明，網絡的特征路徑長度和簇系數都不能單獨決定網絡的同步能力，因為，在兩者都相等的情況下網絡仍然可以有很多不同的配置，因而網絡的同步能力仍然可以存在較大的差異。節點度分布的不均勻性從本質上抑制了網絡的同步能力。仿真結果表明，網絡中節點的最大介數是表征網絡同步能力的一種相對統一的物理量。

參考文獻

[1] NEWMAN M E J.The structure and function of complex networks[J].SIAM Review，2003，45(2)：167-256.

[2] WANG X F，CHEN G R.Synchronization in small-world dynamical networks[J].Bifurcation and Chaos，2002，12(1)：187-192.

[3] LI Z，CHEN G R.Global synchronization and asymptotic stability of complex dynamical networks[J].IEEE Transactions Circuit and System，2006，53(1)：28-33.

[4] WANG X F, CHEN G R.Synchronization in scale-free dynamical networks：robustness and fragility[J].IEEE Transactions on Circuits and Systems I，2002，49(8)：54-62.

[5] ZHAO M，ZHOU T，WANG B H，et al.Relations between average distance, heterogeneity and network synchronizaility[J].Physica A，2006，371(2)：773-780.

[6] WU X，WANG B H，ZHOU T，et al.Synchronizability of highly clustered scale-free networks[J].Chinese Physics Letters，2006，23(4)：1046.

[7] 魏民，王莉，張強.基于復雜網絡理論的典型電力電子電路復雜性研究[J].電子技術應用，2011，37(9)：118-121.

[8] MOTTER A E，ZHOU C，KURTHS J.Network synchronization，diffusion，and the paradox of heterogeneity[J].Physical Review E，2005，71(1)：016116.

[9] NISHIKAWA T，MOTTER A E，LAI Y C，et al.Heterogeneity in oscillator networks: are smaller worlds easier to synchronize?[J].Physical Review Letters，2003，91(7)：014010(1-4).

[10] HONG H，KIM B J，CHOI M Y，et al.Factors that predict better synchronizability on complex networks[J].Physical Review E，2004，69(6)：067105(1-4).

[11] BARAHONA M，PECORA L M.Synchronization in small-world systems[J].Physical Review Letters，2002，89(5)：054101(1-4).

作者信息：

呂  瑛，李穎華

(西北工業大學明德學院 信息工程學院，陜西 西安710124)