一、引 言
回旋行波放大管屬于毫米波放大器件,它以高功率、高效率、寬頻帶而著稱,在雷達與通訊等領域有著極其重要的應用前景,自七十年代末以來,在理論和實驗方面都取得了長足的進展[1~5].
對于基次諧波回旋行波管,在毫米波波段需要很高的直流磁場,因而需要體積較大的超導系統或電磁鐵系統來提供直流磁場.采用高次諧波互作用,便可大大降低管子對直流磁場的要求[2,3],使采用永久磁鐵成為可能,從而可大大減小管子的體積.由于開槽壁和光滑壁波導中高頻場分布存在的差異,開槽波導更有利于注波互作用,對工作電壓要求較低,工作效率比光滑壁波導要高,同時與光滑壁波導相比具有很好的模式競爭抑制能力[6].本文以95GHz開槽3次諧波為例,對回旋行波放大管進行了數值模擬,得到了一些重要的互作用規律.
二、高頻場模式和特性
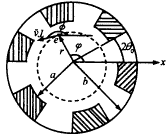
圖1所示為開槽波導結構以及電子注軌跡橫截面圖(虛圓表示電注橫截面圖).設N為開槽波導的槽數,θ0為間隙半張角,a、b分別為波導內外半徑,r、φ、z為電子的柱坐標,v⊥為電子的橫向速度,φ為動量空間角,即v⊥與x軸夾角.為了方便起見,將波導分為兩個區域進行討論,即:Ⅰ區(0<r<a)和Ⅱ區(a<r<b).由于在回旋行波管中電子注與波的有效互作用場為TE波場,故僅需關心橫電波高頻場的分布情況[7~9].這里只給出了高頻電場分量的表達式,有關高頻磁場分量的表達式可進一步能過電磁場分量關系求得.
|
圖1 中空外開槽波導及電子注橫截面示意圖.虛圓為電子注橫截面示意圖 在Ⅰ區(0<r<a)中
在Ⅱ區(a<r<b)中
Ez=0 (4)
其中
在以上各式中,E0為高頻場振幅,Γ為角向諧波數,ΑΓ為角向Γ次諧波項的振幅系數,kc為截止波數,q為開槽序數(q=1,2,…,N),m代表高頻場的角向模式(m=0,1,2,…,N-1).AΓ的值以及電路的色散關系可由電磁場在r=a處的邊界條件確定.
色散關系為
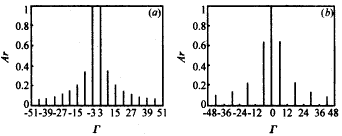
式(9)表明,只有當空間諧波次數Γ=m+lN時,非零空間諧波項才存在.角向模式決定相鄰隙間高頻場的相位差,對于每一具體模式,此相位差值為m2π/N.每一角向模式均由無數個角向諧波項組成,其諧波振幅系數由式(9)決定.在所有角向模式中有兩個比較重要的模式,即π模式和2π模式,其角向諧波相對強弱分布情況見圖2.由圖2可知,2π模式的能量主要集中于零次諧波項中,而π模式的能量主要集中于±N/2次諧波項中.因此,π模式較2π模式更適合于高次回旋諧波互作用.如果電子注回旋諧波次數(用S表示)已經設定,那么槽數N的選擇應保證最強非零次角向諧波項的次數Г與回旋諧波次數S相等.如,對于π模式,槽數N應等于2S. |
|
圖2 角向諧波振幅對角向諧波數(Γ)的相對分布示意圖.(a)π模式(m=N/2,N=6,θ0=15°),(b)2π模式(m=0,N=6,θ0=15°) 當角向模式m和槽深(即a/b的值)確定后,截止波數kc的值可由式(10)通過數值求解方法求得[6,8,9].
三、自洽非線性理論
上述各式中,Cmn為電場歸一化系數,f(z)為一復函數,代表高頻場沿Z軸的緩變分布情況.Cmn的值由下式求得
以下是自洽非線性注波互作用常微分方程組.
以上各式中,m0和γ分別為電子的靜止質量和相對論因子,φ為動量空間角,u=γv,v為電子的速度,如圖1所示.
上式中,P為在一個高頻場周期內所取的電子注批數,M為考慮電子注厚度因數而將電子注化分的圈數,N為每圈上所取的宏電子數,S為諧波次數.〈…〉表示對初始速度分布函數為g0(v⊥,vz)的速度空間進行平均.設電子注為單能電子注,速度零散主要來自于橫縱向速度比值(V⊥/Vz)的零散,這里按正態分布規律來處理速度零散,即初始速度分布函數為
式中K為歸一化常數,△vz為平均縱向速度零散,δ為狄拉克函數.
f(z)|z=0=f(0) (19)
式中f(0)為輸入高頻場電場幅值.
四、結果與討論 表1 數值模擬參數與結果 |
| 內半徑 | 1.024mm |
| 外半徑 | 1.465mm |
| 電路長度 | 87.9mm |
| 注電壓 | 60kV |
| 注電流 | 6A |
| α | 1.3 |
| 直流磁場 | 11.674kG |
| 高頻場模式 | π |
| 諧波次數 | 3 |
| 工作頻率 | 95.08GHz |
| 模擬結果 | |
| 飽和效率 | 22.8% |
| 飽和輸出功率 | 82kW |
| 飽和增益 | 36.15dB |
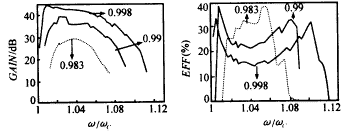
圖6所示為幾個不同磁場失諧率下飽和增益以及飽和效率隨頻率變化的關系.由圖可見,磁場失諧率對飽和增益、飽和效率及飽和帶寬都有較大影響,B0/Bg值的提高有利于飽和增益及飽和帶寬的提高,但飽和效率卻有所降低.在圖示條件下,當B0/Bg值從0.983增大到0.998時,飽和帶寬從4.8%增大到9.3%.
|
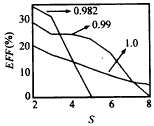
圖6 不同磁場失諧率下,(a)飽和增益及(b)飽和效率隨頻率變化的關系(s=3,π mode,I=6A,V=60kV,α=1.3) 圖7為在不同磁場失諧率下飽和效率隨諧波次數的變化關系.由圖表明,飽和效率隨諧波次數的增大而降低,B0/Bg值越低,諧波次數對飽和效率的影響越大. |
|
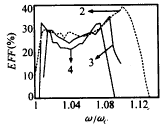
圖7 飽和效率隨諧波次數的變化關系(π mode,I=6A,V=60kV,α=1.3,ω/ωc=γz,rL/a=0.7) 圖8所示為不同諧波次數下飽和效率隨頻率的變化關系.圖示表明諧波次數對飽和帶寬有較大影響.在圖示條件下,諧波次數從2增大到4時,飽和帶寬從10.3%減小到5.7%. |
|
圖8 不同諧波次數下飽和效率隨頻率的變化關系(π mode,I=6A,V=60kV,α=1.3,B0/Bg=0.99,ω/ωc=γz,rL/a=0.7)
五、結束語 |


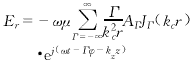 (1)
(1)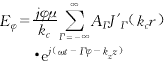 (2)
(2)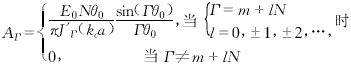 (9)
(9)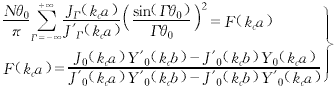 (10)
(10)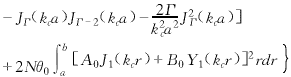 (14)
(14)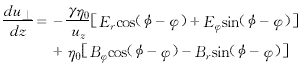 (15)
(15)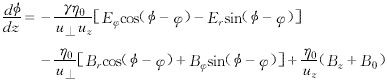 (17)
(17)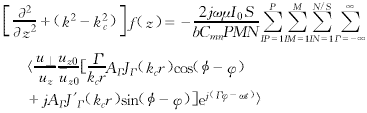 (18)
(18)